![]()
乱数とコンピュテーショナルデザイン
~その1・乱数の種類~
2021.09.09
パラメトリック・ボイス
コンピュテーショナルデザインスタジオATLV 杉原 聡
先日の建築情報学会チャンネルで配信されたSession Vol.5(クリックするとYouTubeへリン
クします)にて稲坂先生も述べられていたように、コンピュテーショナルデザインにおいて乱
数は、設計に多様性を取り入れたりモンテカルロ法のように探索や最適化に用いられたり色々
な場面で利用されている。しかし乱数と一口に言っても様々な種類のものがあり、次に一つ出
力される数がランダムで予測不可能であっても、大局的にはそれぞれ定まった性質がある。ど
のような乱数をどのような設計の場面で、どのような目的で用いるかを考えることは重要なこ
とであり、それについては次回のコラムで記す予定であるが、今回はまず乱数の代表的な種類
を幾つか例とともに挙げる。
規則性が全く存在しない真の乱数とは厳密には異なる。近年は量子現象の観測により真の乱数
を発生する機器やチップも開発され、コンピュータで真の乱数を利用するのも容易になってき
ているが、規則性が無いという点が重要な相違点であり、統計的性質は疑似乱数と違わないと
考えられる。統計的性質の異なる代表的な6つの乱数、一様分布乱数、三角分布乱数、正規分
布乱数、ベータ分布乱数、ガンマ分布乱数、カイ二乗分布乱数と、統計的性質とは別の観点で
異なるパーリンノイズとランダム・ウォークについて以下に述べる。
一様分布乱数
一様乱数とも呼ばれるこの種類は最も一般的に用いられる乱数であり、図1のヒストグラムに
見られるように定められた区間の全ての数が等しい確率で出現し、その結果平均は区間の半分
の値となり、区間が0から1であれば平均は0.5である。
なお図1の生成にはNumPyのrandomモジュールのuniform関数を用い、ヒストグラムは長さ
30000の数列の結果、2次元点プロットとボロノイ分割には長さ500の乱数列2つをX座標、
Y座標にそれぞれ用い、50x50のグリッドのRGB色列には長さ2500の乱数列3つをR、G、Bそ
れぞれに用いた。

図1:一様分布乱数 (左より乱数列プロット、ヒストグラム、2次元点プロット、ボロノイ分割、
RGB色列)
三角分布乱数
三角分布乱数は、区間の両端点を0とし区間内のある点を頂点とした直線的な確率分布に従っ
て生成される乱数列である。図2ではNumPyのtriangular関数を用い、区間は0から1, 頂点は
0.5の位置にあり、生成される乱数の平均値は0.5である。中央の値の頻度が両端よりも高いた
め一様分布乱数に比べるとRGB色列がグレーに寄っている。

図2:三角分布乱数
正規分布乱数
ガウス分布乱数とも呼ばれるこの種類はネイピア数eを底とする指数関数で表されるガウス関
数に確率分布が従う乱数列である。図3ではNumPyのrandn関数を用い、その平均値は0、標
準偏差は1であるが、図の作成過程で値は区間に応じて再正規化(Grasshopper的に言うならreparameterize)され、0から1の区間で平均は0.5である。平均値への集約具合は標準偏差に
よって制御されるが、以下の図3のケースでは三角分布よりも更に中央へ寄っており、RGB色
列も更にグレーに寄っていることが見て取れる。

図3:正規分布乱数
ベータ分布乱数
これは多項式で表される確率分布のベータ分布に従う乱数である。
図4ではNumPyのbeta関数を用い、そのパラメータαには2、βには2を使った。このときの分
布曲線は放物線と一致し、分布の平均は0.5である。三角分布乱数と正規分布乱数と比べると、
平均への集約度は弱まっているが、一様分布乱数ほどには区間の両端に値が生成されていない
ことが、2次元プロットの4つの辺の近辺と、RGB色列の鮮やかな色の少なさから見て取れる。

図4:ベータ分布乱数
ガンマ分布乱数
これは多項式と指数関数を組み合わせた確率分布のガンマ分布に従う乱数である。
図5ではNumPyのgamma関数を用い、そのパラメータkには5、θには1を使い、この場合平均
値は5であるが、区間は正の方向に開いており、図の生成で用いた長さ30000の数列での最大
値は13.1である。これらを0から1の区間に正規化すると平均は約0.38となり、2次元点プロッ
トと、RGB色列に偏りが見て取れる。

図5:ガンマ分布乱数
カイ二乗分布
これは多項式と指数関数を組み合わせ、母数 kで定められる確率分布のカイ二乗分布に従う乱
数である。
図6ではNumPyのchisquare関数を用い、その母数kは3を用い、この場合平均値は3であるが、
区間は正の方向に開いており、図の生成で用いた長さ30000の数列での最大値は19.5である。
これらを0から1の区間に正規化すると平均は約0.15となり、2次元プロットと、RGB色列にも
大きな偏りがある。

図6:カイ二乗分布乱数
パーリンノイズ
パーリンノイズは元来コンピュータグラフィックでのテクスチャ生成のために開発されたアル
ゴリズムであるが、乱数列として見ると隣り合う数の勾配に制限がある乱数列として見える。
通常の乱数列には前後の数の間に関連性は一切無いが、パーリンノイズは関連性があるため数
列空間での位置を入力して特定の場所の乱数を得る。1次元である数列の空間に対するパーリン
ノイズだけでなく、入力空間として2次元、3次元をとる2次元、3次元パーリンノイズもある。
図7ではProcessingのnoise関数を用いて乱数を生成した。トップダウンに計算された乱数列で
あるためかヒストグラムのように正規分布に似た分布と平均値に収束している。1つ目のRBG
色列は1次元パーリンノイズをX方向に並べたものであり、2つ目のものは2次元パーリンノイズ
によりRGBそれぞれが指定された色列である。
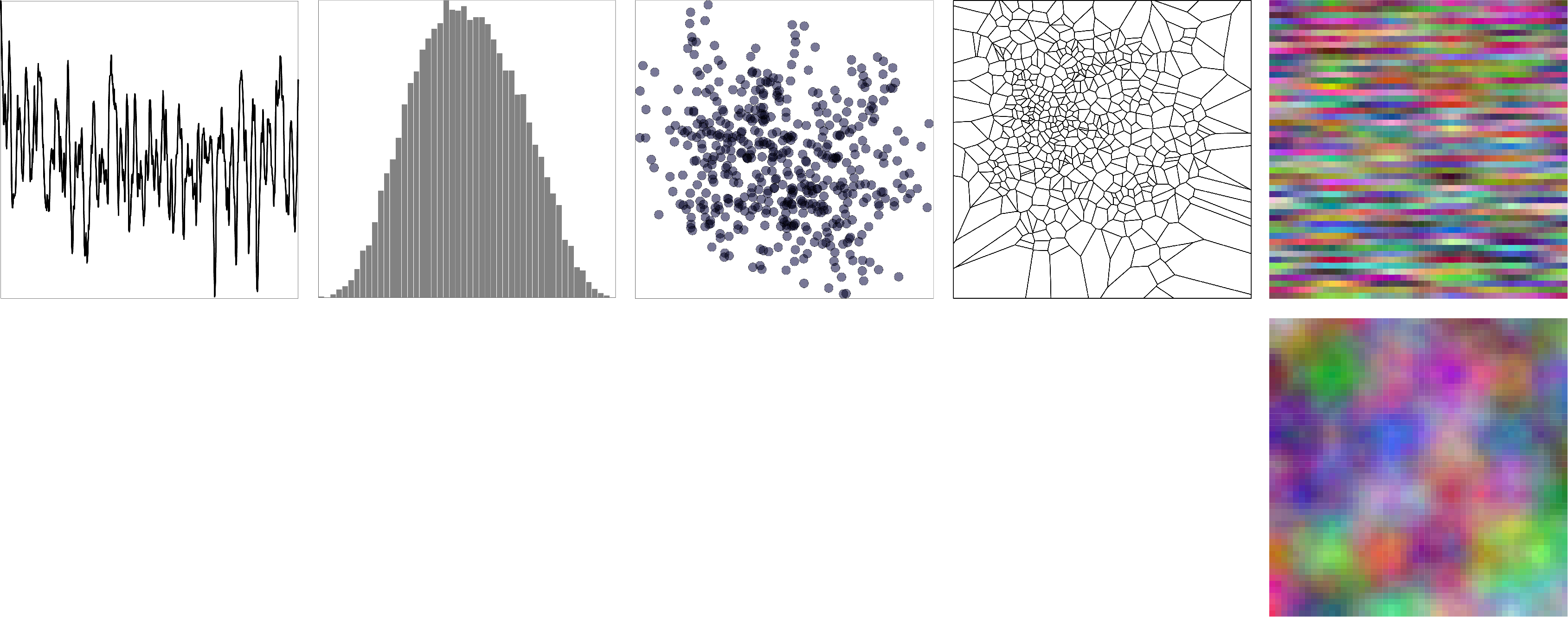
図7:パーリンノイズ
ランダム・ウォーク
ランダム・ウォークはブラウン運動などの自然現象をシミュレートする数理モデルで、一つ前
の数列の値に乱数を加えたものを次の値とする数列である。最も単純な形式は前の値に-1また
は1を等確率で加えるというものであるが、図8では上でも用いた平均を0とする正規分布乱数
を前の数に加えたガウス・ランダム・ウォークを用いた。ランダム・ウォークはパーリンノイ
ズと同様に数列の前後に関係性があり、変化の幅は制限されている。しかしこの数列はひとつ
ひとつボトムアップに計算されており、一定の分布に収束しない。図8を他の図と比べてもそ
の性質の違い、特にその不均一さが見て取れる。これは見方によっては局所性とランダム性を
持つそれぞれの仕組みを2段階の階層で組み合わせたものと考えることもでき、上に記した分
布によって定義される乱数とは仕組みが異なっていると考えられる。

図8:ランダム・ウォーク
以上に代表的な乱数の種類を挙げたが、次回のコラムでは設計において乱数を利用することの
利点、注意点、功罪などについて述べたく思う。



























