![]()
乱数とコンピュテーショナルデザイン
~その2・設計における乱数の利用~
2021.11.09
パラメトリック・ボイス
コンピュテーショナルデザインスタジオATLV 杉原 聡前回のコラムでは乱数の種類について述べたが、今回は設計における乱数の利用について記す。
最初に、幅が100の領域を横方向に100分割することを考える。図1aは領域を100等分してい
るが、図1bは0から100までの値の一様乱数を座標値とする位置に分割線を引いている。この
場合、一つの分割された領域を定める左右の分割線の位置に関連性は無く、ほぼ同じ位置に分
割線が現れて極めて小さな領域が作られることもあれば、逆に大きな領域が作られることもあ
る。また一様乱数の性質から、分割線の位置の平均が50の位置になる。図1cは、図1aのよう
に100等分した後に、-0.5から0.5の一様乱数によって分割線を左右に移動したものである。最
も右に移動した分割線と最も左に移動した分割線で小さな領域が作られることはあるが、大き
なものは最大でも幅2であり、一様乱数性質から分割領域の幅の平均は1となる。図1dはランダ
ム・ウォークにより生成された数列を0から100にスケールしなおした値を分割線の位置とした
ものである。ランダム・ウォークはランダムな位置からスタートして差分に一様乱数が用いられ
ており、一様乱数に見られるような安定した統計的性質が現れず、分割線の位置や分割幅に安定
した傾向が見られない。

図1.乱数を用いた横方向の分割
次に乱数を用いて正方形の二次元領域を100の領域に分割することを考える。上記の一次元領
域の分割では、図1bとcのように乱数を位置に用いるか、それとも幅に用いるかで結果に違い
が出た。二次元領域では何に対して乱数を用いるかの選択肢はより多くある。図2aは縦横10等
分したものであるが、分割領域の幅に対して一様乱数を用いると図2bのようになり、高さに対
して用いれば図2cのようになる。今度は、分割領域の幅と高さ両方に乱数を用いることを考え
る。ここで分割領域の重なりと隙間は許容しない事とし、分割領域は矩形とする。この条件は
強い拘束条件であり、ランダムな幅と高さの矩形を敷き詰めて隙間も重なりも無く正方形全体
を埋めるのは容易ではない。全ての幅と高さが異なる訳ではないが、同一の列内の高さは同じ
にすると、縦方向を一様乱数で分割して各列の高さを決め、それから横方向をランダムに分割
する図2dの方法がある。また、もしも縦の分割線を連続させ、縦横隣り合う矩形の角が同一の
点で接するという条件が追加されると図2eのような分割方法がある。
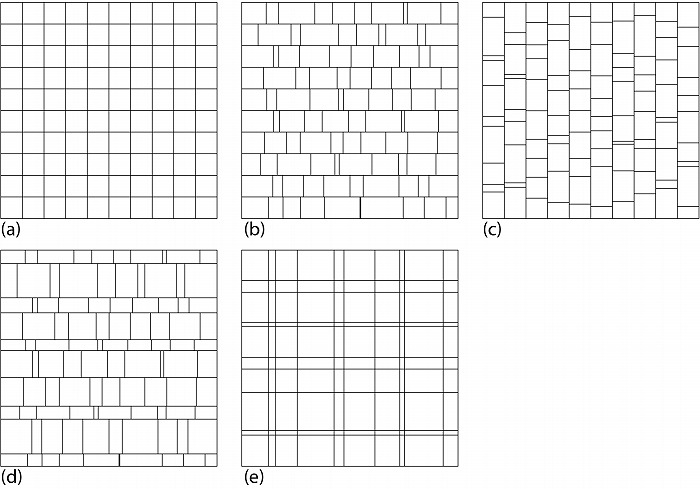
図2.正方形のランダムな分割その1
今度は分割領域の寸法ではなく、分割数に乱数を用いることを考えると図3aのような、横方
向に等分はしているが、各列の等分数が整数の乱数で与えられるものを考えることができる。
また、大半の矩形の縦横寸法を同一にしたとしても、各列の端の領域のみランダムな幅とする
ことで列毎にずらした分割が可能になる(図3b)。それから乱数を用いる場所を選ぶという選
択肢もある。図3cでは一度等分した分割線を横方向に一つ飛ばしで選び、選んだものだけを
左右に一様乱数で移動している。また図3dでは一つ飛ばしで選んだ領域の幅はランダムにし
ているがそれ以外を一定の幅としている。図3eでは一様乱数による分割線の左右移動量を上
部では少なく、下部では多くなるよう調整している。
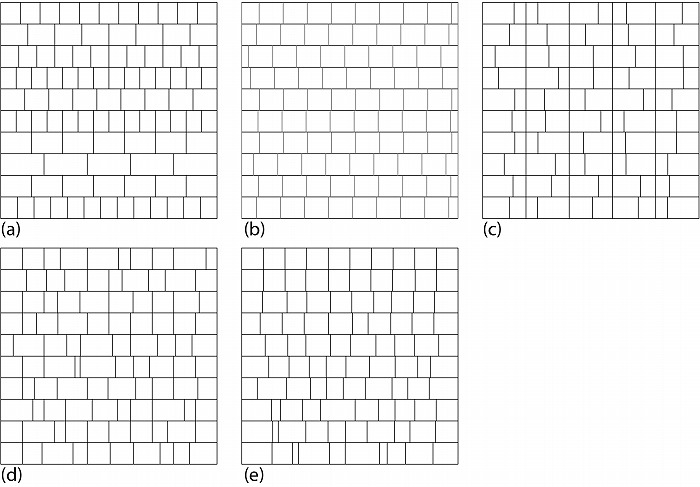
図3.正方形のランダムな分割その2
また、限られた種類の分割領域形状をランダムに選ぶという方法も考えられる。図4aでは幅
の広いものと狭いものをランダムに選択して横に並べている(一つの列には広いもの・狭いもの
各々五つという条件も課している)。図4bでは横に並んだペアと縦に並んだペアをランダムに
選択している。分割領域形状を三角形とするのであれば、等分した矩形領域を更に分割する対
角線の方向をランダムに選んで図4cのような分割方法も考えられる。図4dのように、分割領
域は台形となるが、分割線を移動ではなくランダムな角度で回転するという方法もある(この場
合一つ飛ばしで分割線を回転している)。また図4eでは分割線の回転角度を-36°、0°、36°の
3種類の中からランダムに選んでおり、限られた種類の矩形や台形の領域が現れる。回転角度を
-45°、0°、45°にして分割線の端点が他と一致する回転であると、タングラムのような三角形、
矩形、平行四辺形、台形の領域で全体が構成できる(図4f)。
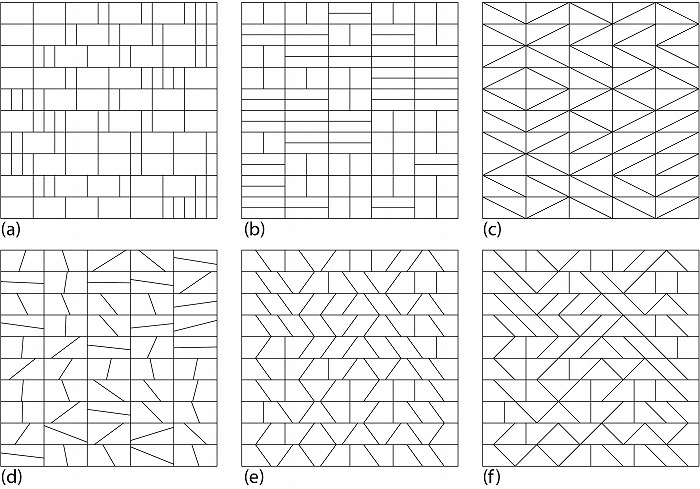
図4.正方形のランダムな分割その3
更に回転角度0°と45°のみにすると、図5aのような平行四辺形、正方形、台形のパターンとな
り、45°、-45°とすると図5bのように三角形、平行四辺形、両端の台形で構成でき、連続する
分割線により特徴的な斜めのパターンも現れる。また2種類の斜線の代わりに4種類の円弧を用
いると図5cのようなパターンが現れる。
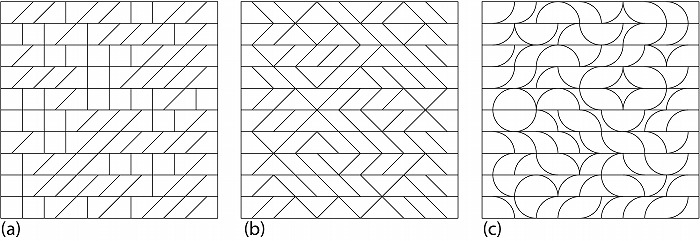
図5.正方形のランダムな分割その4
また限られた種類の形状をランダムに並べて現れる知られたパターンとして、図6cのようなも
のがある。図6aのように正方形の対角上の円弧対と、逆側の対を格子上にランダムに選んで並
べると、円弧が滑らかに連なり(図6b)、図6cのようなパターンが現れる(世代問題はあると思う
が私は個人的にチクタクバンバン・パターンと呼んでいる)。通常このパターンは領域分割には
使われず、分割はユニットの正方形で規則的に行った上で、円弧はグラフィカルなパターン表
現に用いられる。だが円弧のパターンを領域分割に用いることも可能ではあり図6cでは100個
の領域に分割されている。だが円またはその一部の小さい領域がある一方、枝上に連結した巨
大な領域も発生しえてパネル化のための分割には適さない。このようなパターンの構築には、
図6aのユニットの正方形四辺の各中点を通る線であれば何でも可能であり、例えば斜線で繋ぐ
と図6dのようなパターンとなるし、ユニットの種類も2つである必要は無く、縦横の線でつな
いだ4種のユニットを用いると図6eのパターンが生成される。図6fはユニットは2種類だが一
つのユニットは図6aのようにユニット領域を(斜線で)3つに分割している一方、もう一つはユ
ニットを円弧2つで4つに分断しており、分割領域が連続して大きくなりすぎない傾向がある。
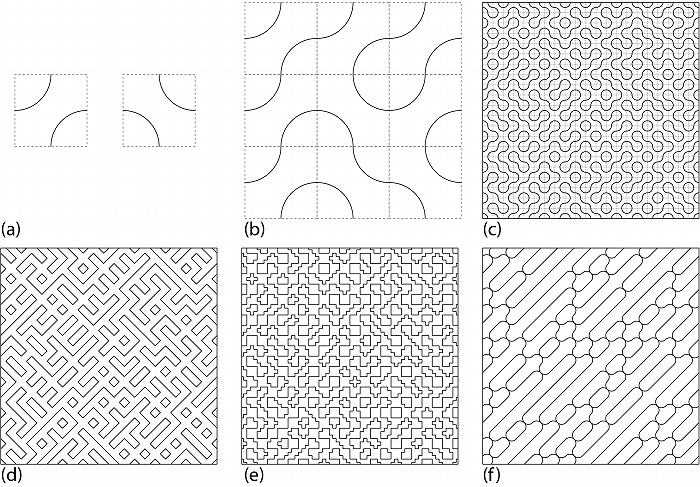
図6.正方形のランダムな分割その5
図7aでは縦の分割線を回転ではなく、上下端点それぞれをランダムに左右に動かして斜線にし、
多様な台形領域を生成している。縦方向の分割線を分断せず、図2eと同様隣接する4つの分割
領域の角を一致させるのであれば図7bのような分割となる。縦方向も横方向も分割線を連続さ
せたまま、それらの交点を左右だけでなく上下にも一様乱数を用いて移動させたのが図7cであ
り、各分割領域は不定形な四角形となる。しかし乱数による移動量が大きすぎると図7dのよう
に分割線が交差して領域の重なりが発生し、分割としては不適切となる。図7eでは、乱数によ
る移動量を周縁部では少なく、中央では大きくなるよう連続的に調整されている。
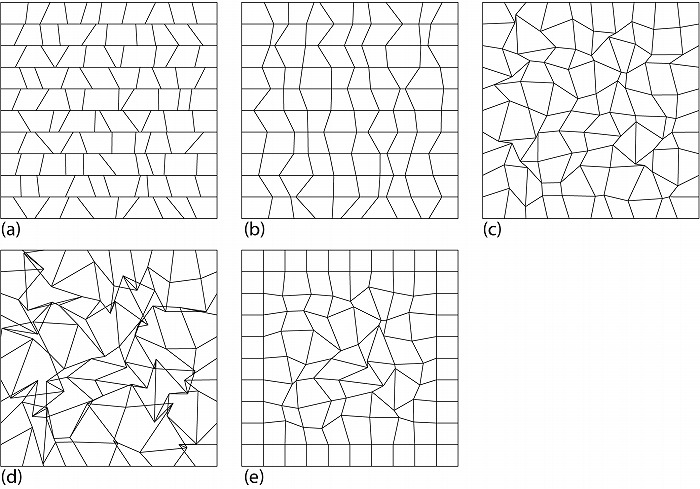
図7.正方形のランダムな分割その6
また再帰的に矩形を縦か横に分割することによって図8aのような矩形分割も可能である。これ
は縦長の矩形は縦に分割、横長のものは横に分割するという条件を付けているが、その条件を
無くすと図8bのような縦か横に極端に長い矩形も発生する。また図8aとbは面積が大きい矩
形を常に優先して分割しているが、その条件を無くすと図8cのような大きさのばらついた分割
となる。縦長/横長の条件も、面積に関する条件もどちらも無くランダムに選んだ矩形を、再帰
的に縦か横にランダムに分割すると図8dのようにばらつきは更に増す。矩形を二つに分割す
る代わりに、四畳半の畳のように五つに再帰的に分割した場合は図8eのように分割される(分
割領域数を100とするため最初に4分割されてから再帰的に5分割されている)。
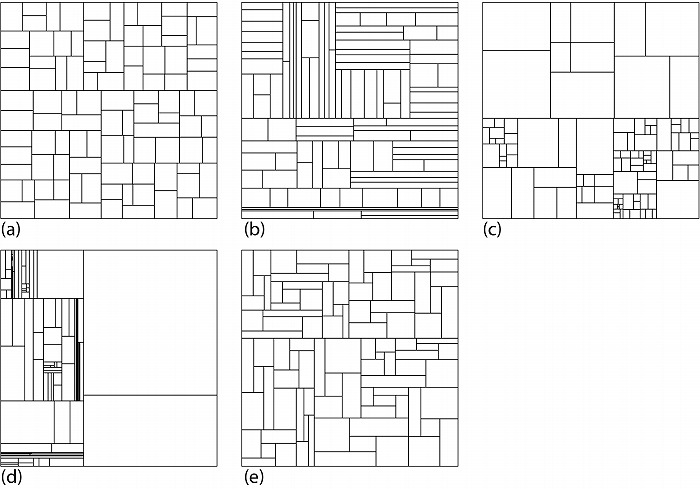
図8.正方形のランダムな分割その7
三角形の領域にランダムに分割するのであれば、ドロネー三角形分割が有名である。任意の点
集合の間に線を引いて図9aのように三角形分割できる。またドロネー三角形分割を元に(不定
形であっても)四角形の領域に分割したいのであれば図9bのように隣り合う三角形を組み合わ
せれば良い。任意の点集合から領域に分割するもう一つ有名な手法はボロノイ分割(図9c)であ
る。ボロノイ分割では分割線は入力点の上を通らず、点とその近傍点の間に垂直二等分線が分
割線となって不定形な凸多角形の領域が形成される。ドロネー分割もボロノイ分割も、入力の
点集合に対して一意に分割が決定するので、点集合の傾向が変われば分割の傾向も変わる。
図9a~cで用いられた点集合は規則的に格子上に並んだ点集合を上下左右に(図7cのように)
一様乱数で移動したものである一方、図9dは一様乱数を縦横の座標値に直接用いた点集合を
入力としている。図9cでは分割領域の大きさと分布にある程度一貫性が見られるのに対し
図9dは大きさにも密度にもばらつきが見られる。これは図1cとbの違いに相当する。また点
集合のランダムさを図3eのように連続的に調整(格子上の点の移動量をゼロから最大値まで連
続的に調整)すると、図9eのように格子分割からボロノイ分割に移行するような方法も可能と
なる。ボロノイ分割は特徴的な凸多角形領域を生成するが、その分割線を縦横の線に変換して
図9fのような不定形ではあるが縦横直交した線で構成される領域への分割も可能である。
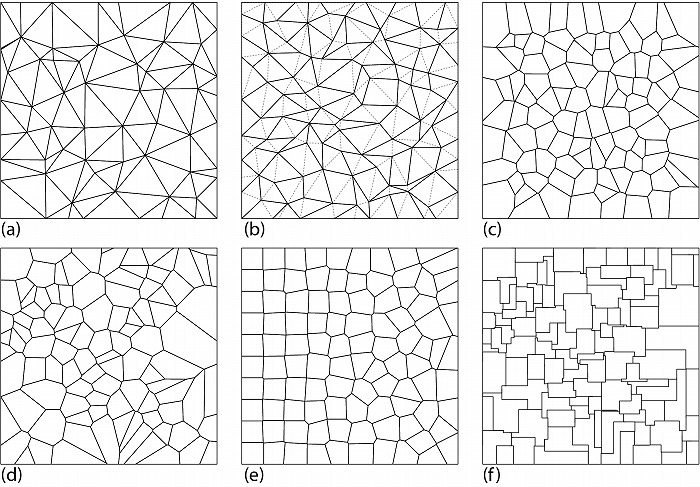
図9.正方形のランダムな分割その8
以上見てきたように、乱数を用いて領域を分割する方法は、どこにどのように乱数を用いるか
によって無数に存在する。分割に限らず設計において乱数を用いる場合でもそれは同様であり、
どこにどのように利用するかをしっかり考えることで乱数の創造的な利用はいくらでも可能で
ある。また異なる方法によってもたらされる結果にはそれぞれ異なる心象的特徴や素材/構造/
製造/施工上の長所・短所があり、それらをよく検討することが重要である。
過去にグラスホッパーで、その開発者が冗談でつけたボロノイ使いすぎ警告機能が話題になっ
たことがある(現在のバージョンでもその機能は存在する)。これは当時のバイオミメティクス・
デザインの潮流と、ボロノイ・ツールの使い易さから、無自覚にボロノイを設計に利用する人
が増加したことに対する警鐘として作られた。また目新しいツールを使って流行りに迎合せず
とも、周りの人間に対する無自覚な迎合から、規則性の高いまたは個性の低い設計を提案する
ことも、一つの正しい解が存在しない設計の世界では同様の罪である。設計案の検討のために
色々なツールを使い様々な方法を試すことは大いに推奨されることである一方、特徴・長所・
短所の検討と、なぜその設計にするかの自問自答は十分になされなければならない。それらに
対して無自覚なまま設計を提示することは設計者として無責任であり、自動ツールが溢れる昨
今であっても、なぜその設計を選んだか/なぜそのようにしたかを自覚して設計を行うことは
設計者並びにクリエイターの責任であると私は考える。



























