前回のコラムに引き続き、設計の合理化手法について述べる。今回は合理的曲面分割について
記す。

円柱・円錐面の合理的曲面分割
　
円に対して軸が垂直な円柱・円錐面は円周沿いに均等に曲面を分割することにより容易に同一
形状のパネルを繰り返すことができるが(図1a、図2a)、円と軸が垂直でない斜円柱や斜円錐や、
分割線が円に平行でない場合は同一形状とならず、その形状は異なる平行四辺形(図1b、図1c)
または台形(図2b、図2c)となる。円と軸は垂直だが分割線が円に対して斜めである場合 (図1c)
は、円周の等分により分割されたパネルは、形状は異なるが幅は同一となる。また円に対して
斜めの境界線を持つ円柱・円錐面に、円に並行な分割線を引き直すことによって同一形状のパ
ネルを繰り返すことができるが(図1d、図2d)、上下の境界線付近に不規則な形状のパネルが生
成される。

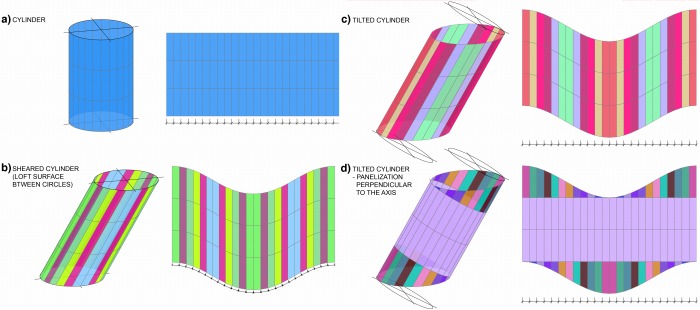
　図１　円柱面の曲面分割

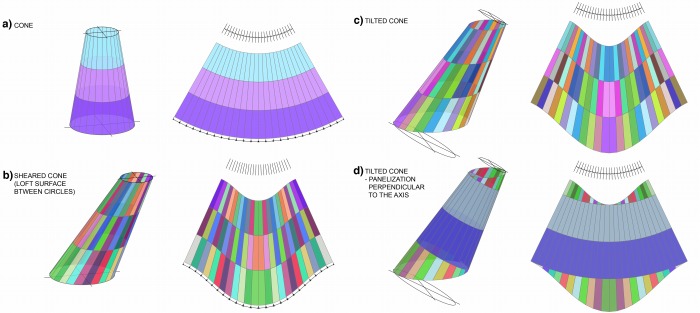
　図２　円錐面の曲面分割

この知見のプロジェクトへの応用例として、ファール・タワーのガラス面の分割について述べ
る。初期の分割方法は、タワーの構造である斜め格子の中心線を曲面に投影することによって
まず三角形の平面領域に分割し、その次にガラスパネルとして適切な矩形に近い形状に分割す
る案であった(図3左)。しかしこの方法では斜め格子の線が交差する点の近傍で、鋭角三角形
パネルが数多く生まれる。角が鋭すぎるガラスパネルは強度の問題から代わりに金属パネルを
嵌めることとなり、見た目が継ぎ接ぎになり透明性が失われる。このような三角形パネルの数
を最小にするために曲面の分割方法を見直した。タワーの角の丸まった形状を全て円柱、斜円
柱または斜円錐で近似し、上記の曲面分割手法で合理的に曲面分割を行った(図３中、右)。こ
れにより曲面上のガラスパネルの多くを矩形、平行四辺形または台形のパネルで構成すること
ができた。なお、このように円柱、斜円柱、斜円錐近似を無理なく行えたのは、前回のコラム
で触れたように、もとのタワー形状がフィレット操作により生成されており、形態に合理性が
内包されていたためである。

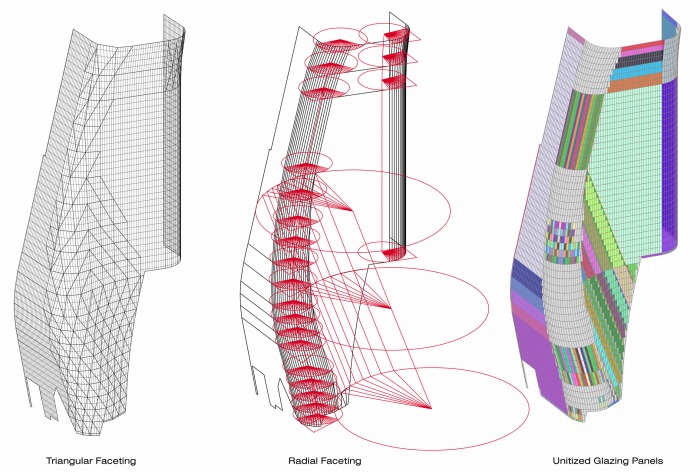
　図３　ファール・タワーのガラス面の合理的曲面分割（設計：Morphosis）

パネル間の角度の合理化
 
図３に見るようにファール・タワーの右側の角の大半は円柱面となっている。この円柱面の中
心と半径は円弧の端点が内部グリッドと一致するように調整されているが、この円弧を等分し
てガラスパネルを分割生成すると、図４左のように円弧内のパネル同士の間の角度は全て同一
の角度(2A)となるものの、円弧の端にあるパネルとその隣の平面上にあるパネルの間の角度は
90°+Aと異なってしまい、２種類の異なる断面のマリオンが必要になる。だが、中心から円弧
端点への線の２等分線上に新たな中心を置き、端点接線が平面の直線と一致しないやや大きな
円弧を描くことによって、端のパネルとの角度も円弧内のパネル間の角度と同一の2A’とするこ
とができ、1種類のマリオンのみで構成できる。

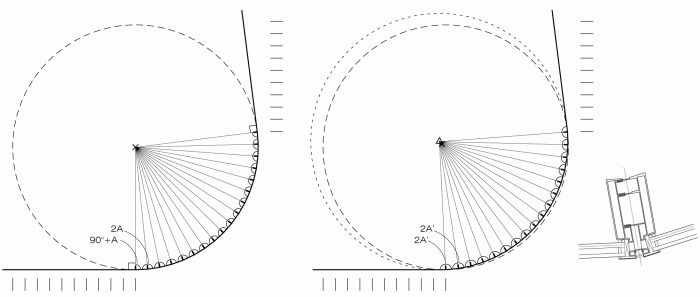
　図４　円柱面のパネル間を同一角度にする分割方法

斜め格子構造のための合理的曲面分割
 
図５にファール・タワーの斜め格子構造の合理化のプロセスを示す。最初に斜め格子構造は物
理シミュレーションを用いたメッシュ・リラクゼーションによって滑らかに繋がるよう生成さ
れた。しかしそれだと格子上の柱の長さがほぼ全て異なり合理的ではない。そのため柱の長さ
及びその間の三角形形状をできるだけ同一となるよう合理化を図った。合理化はタワー形状の
曲面上に同一形状を手動で繰り返し、また異なる同一形状領域の間は、接線の角度差を最小化
するメッシュ・リラクゼーションを用いて縫い合わせた。これにより、異なる形状の領域の間
も境界が目立たず滑らかに繋ぐことができた。なお図５右2つの合理化で斜め格子が急激に変
化しているのは次の理由による。鉄に強い構造事務所と取り組んだコンペ時に、複曲面を持つ
タワー形状の構造は斜め格子によるシェル構造とするのが効率的と提案されたが、コンペ後に
組んだコンクリートに強い構造事務所はコンクリートのエレベーター・コアを主要な構造とし、
先細る上層階には横荷重は少ないため斜め格子は必要無いと提案された(中・下層部左の複曲面
の部分は依然として斜め格子が効率的)。更に現地の法令は柱の最小断面寸法を定めており、斜
め格子は理論的には2本で1本の柱と等価の機能を果たすため、太さは通常の柱より細くできる
はずであるが、法令上は独立した1本の柱と見なされ、必要以上の寸法が求められてしまう。
しかし2方向に走る斜め格子の一つを垂直に、もう一つをより斜めにすると、法令上一つは柱、
もう一つは筋交いと見なされ、筋交いに要求される寸法は柱より遥かに小さいため、必要とな
る建材とコストを削減でき、最終的に図の右のように合理化された。

　図５　ファール・タワーの斜め格子構造の合理化プロセス

合理的分割の可視化
 
図3や図5のように同種のパネルに同じ色を付けることによる合理性の可視化は、パネル形状と
寸法を比較して色付けするコードを作成して自動で行っている。このような可視化は、第一に
設計がどの程度合理化されているかをプロジェクトに関わる人に視覚的に伝達し理解してもら
うのに役に立つ。第二に合理化をコンピュテーションや定まった手順で行っている場合にどの程
度合理化がなされたか結果を自分で確認することに役立ち、第三にパネル寸法の同一性比較は
ある許容値幅を持って計算するため、許容値の幅を少し増やすことにより、同一形状に近似で
きる可能性がある別のパネルを表示することができ、合理化の改善可能性を設計者に示唆する。
 
合理化と心理効果
 
図6は、図3で合理的に分割されたガラスパネルを展開し同種のパネルの数を記述したものであ
る。これは上記の可視化と同様に展開、色付け、数え上げを行うコードを作成して自動化され、
伝達・確認・改善の示唆の役割を担っているが、展開図ではより具体的な形状と数が示されて
おり更なる理解と伝達が行える。建設工事の入札において、建設業者は主に図面の設計情報に
基づき入札価格を算定するが、入札の時点で全ての設計が細部まで詰められているとは限らな
いため(また詰めすぎると業者ごとに異なる効率的な建設方法を許容する柔軟性が失われるた
め)、詰められていない点や不明瞭な箇所の算定は予期せぬ状況を加味した安全率が乗算され
て入札価格に加算される。図3や図6のような可視化ダイアグラムを図面に含めることにより、
形状やパネルの種類の複雑さによる不明瞭さは減少可能である。また図3における、合理的に
見えても困難な形状がどこかに隠れているかもしれないという心的印象を、図6で困難なもの
を含んでパネル形状を全て列挙することで払拭しているように、これらのダイアグラムはどの
程度合理化がなされているかを伝えるだけでなく、最も困難な箇所を明示して困難さの程度を
明確にすることで、実際以上に困難そうである心的印象を和らげ、安全率を下げることに役立
つ。このように合理化とその可視化は、理解の促進による建設コストの削減に繋がる。

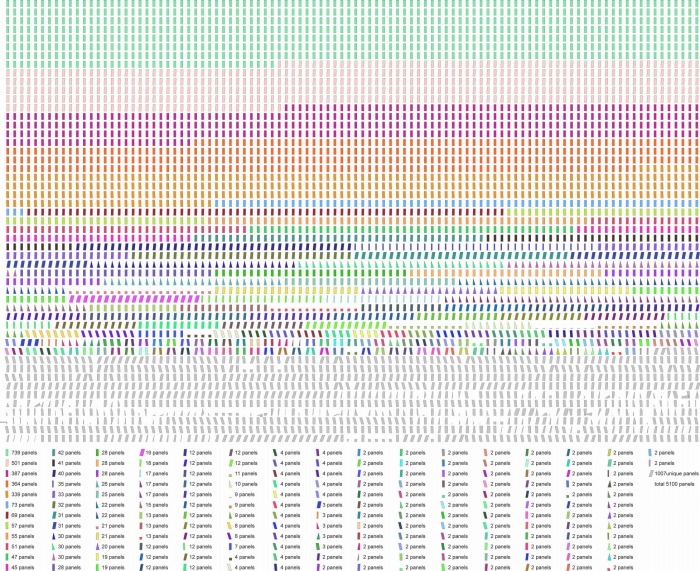
　図６　ファール・タワーのガラスパネルの展開とパネル・ユニット数

以上今回はファール・タワー・プロジェクトを例として曲面の合理的分割について述べた。文
章が長くなったため、設計の合理化のもう一つのトピックである部材のユニット化については
次回に譲ることとする。