![]()
形状を統合するアルゴリズムのデザイン
2023.11.14
パラメトリック・ボイス
コンピュテーショナルデザインスタジオATLV 杉原 聡ある形状と別の形状を補間により統合してその間の形状を自由に生成できるアルゴリズムにつ
いて考える。
例えば丸と四角を補間して統合したいとき、Rhinoceros Grasshopper上ではLoftを用いて以
下のようにできる(図1)。ここでは閉曲線で表される二つの形状を入力にとり、片方の曲線
をZ方向に移動してからLoftし、その間を平面と交差させXY平面上に戻すと二つの形状の間の
形状が生成できる。
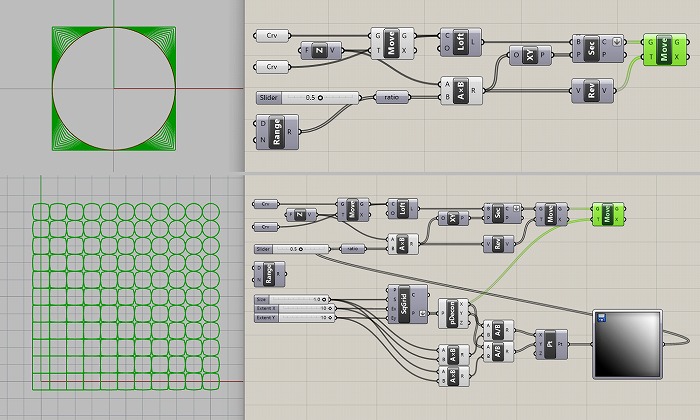
図1. GrasshopperにおけるLoftを用いた二つの閉曲線形状の統合と、画像入力による形状生成
しかし、入力の曲線またはその向きによっては図2のような異なる形状が生成される。これは
GrasshopperでLoftを実行する際、内部では一つ目の曲線のどの点が二つ目の曲線のどの点に
繋がるかを決定しており、図2ではそれぞれ入力曲線の始点が異なる場所にあり、曲線の始点
同士がLoft時に繋がっているためである。なお、GrasshopperのLoftコマンドのAlign sections
オプションは、繋げる箇所を始点同士ではなく距離の近い箇所にとることによって自然な形と
する。また図2ではLoftの結果四つのNURBS曲面からなるPolysurfaceが生成されているが、
LoftコマンドのRebuildかRefitのオプションを選択すると一つの近似曲面が生成される。この
とき入力曲線の制御点が内部で再構成され、二つの入力曲線の制御点が同数に揃えられる。
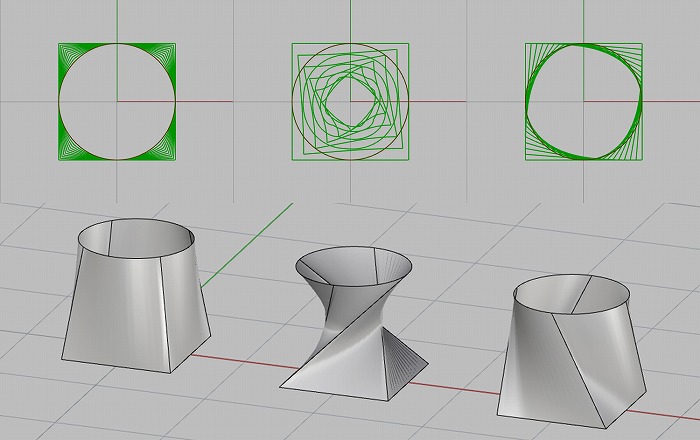
図2. 異なる統合結果とそのLoft形状の違い
上記で見て取れるように、補間により統合する方法は一つではない。映像の分野で用いられる、
一つの画像を連続的に別の画像に変化・変形させるモーフィングもこのような形状の補間と類
似した手法であり、そこでも元の画像のどこがもう一つの画像のどこに対応するかによって、
変化・変形の過程は異なる。形状を統合するアルゴリズムの設計においては、この対応関係を
考えることが重要である、というのが今回のコラムの主旨である。対応関係を考えるのは、幾
何学要素に対してであり、それは点であったり、辺であったり、面であったり、立体であった
りする(図3)。
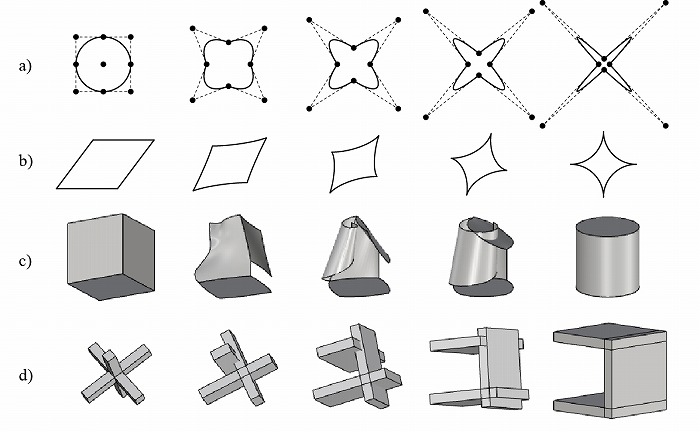
図3. 統合する対象:a) 点(制御点)、b) 辺、c) 面、d) 立体
このような要素の対応関係を考えるとき、要素の数に応じて大きく二種類の場合がある。一つ
は対応させる要素の数が一致しているとき(図4)、もう一つはしていないときである。図4
では同数のパネル数を生成する矩形パネル化アルゴリズムと三角パネル化、円を詰め込んだパ
ネル化、ボロノイ・パネル化アルゴリズムが統合されている。要素の数が一致しているとき、
統合の設計で考えるのはどの要素がどの要素と対応するかの順番であり、それに応じて結果は
異なる(図5)。

図4.同数のパネル形状の統合したパネル化アルゴリズム例
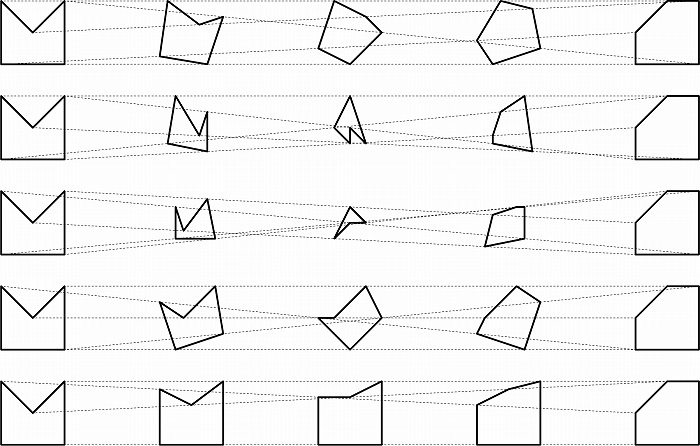
図5. 辺の数は同じで対応する順が異なる統合例
統合しようとする要素数が異なっている場合には、Loftコマンドが内部で自動的に行っていた
ように、その数を揃えなければならない。要素の数を揃えるには以下の三つの方法が考えられ
る。
一つ目は要素を分割または接合して数を揃える方法である。図6では辺の数の異なる形状に対
して、辺が少ない時に分割して増やしたり、多い時に辺を結合して減らしたりして数を揃えて
いる。図6aでは円を四つの円弧に分割して、図6bでは三角形の一辺を分割して四角の辺と対
応させている。図6cでは三角の三つの辺が五つに分割された後二つは接合して四角の四つの
辺となり図6dは五角形の五つの辺のうち二つが接合して四辺となっている。
図7では一つの領域が二つに分割される例(図7a)、三つの領域が一つに接合する例(図7
b)、四つの領域が六つに分割され、それから三つに結合する例が示される(図7c)。図8aは
矩形パネル化アルゴリズムを水平に二分割することで三角パネル化アルゴリズムと統合した
例、図8bは矩形パネル化アルゴリズムと斜めの六角形パネル化アルゴリズムを分割と接合に
より統合した例である。
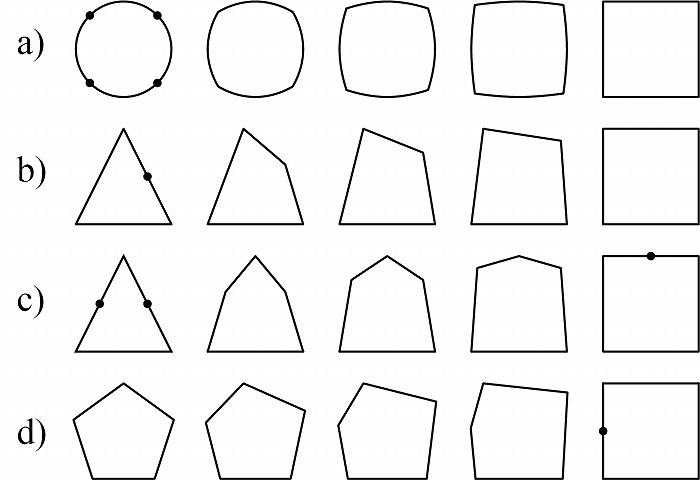
図6. 辺を分割または接合して辺の数を合わせた例。点の位置で分割または結合されている
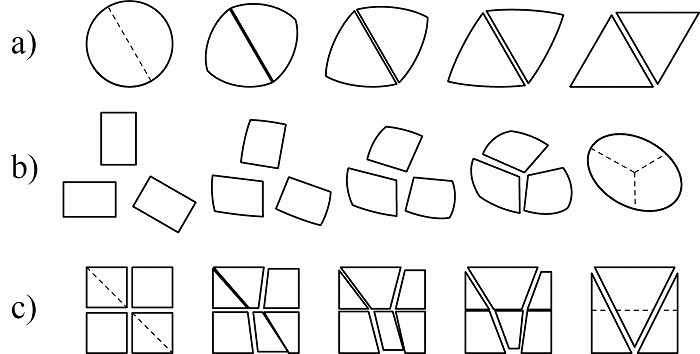
図7. 領域を分割または接合して数を合わせた例
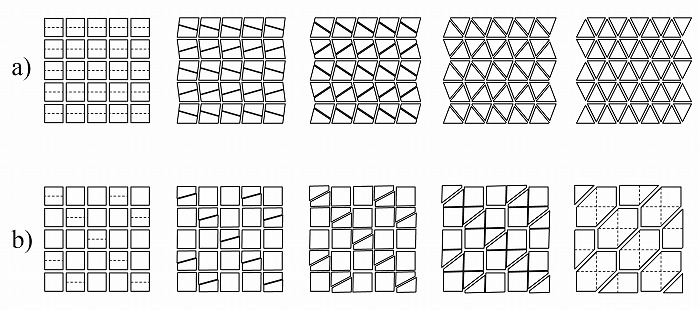
図8. 分割または接合によるパネル化アルゴリズムの統合
二つ目の方法は、足りない要素を生成したり、多すぎる要素を消滅させて数を合わせる方法で
ある。図9a~dは三角形と四角形を統合する例で、図9aと図9bは赤い点から辺を生成して四
角形の四つの辺と数を合わせている。図9cは2点より辺を生成し、なおかつ 2辺は接合して
一つの辺になっている例である。図9dでは三角形領域全体が点へ消滅する一方、点から四角形
全体が生成されている。図9e~hでは円と四角を統合する例で、図9eでは赤い点から辺を二つ
生成して四角の四つの辺と合わせており、図9fでは、四つの赤い点から直線の辺を生成する一
方、青い四つの弧を点へ消滅させている。図9gとhでは厚みのない赤い線から四角を生成する
一方、青い円を線へ消滅させている。図10は矩形パネル化アルゴリズムと斜め格子(図10a)、
六角形グリッド(図10b、c)、ドロネー分割(図10d)などを領域の線への消滅と線からの生
成を用いて統合した例である。ちなみに図10bは領域の接合も用いられている。
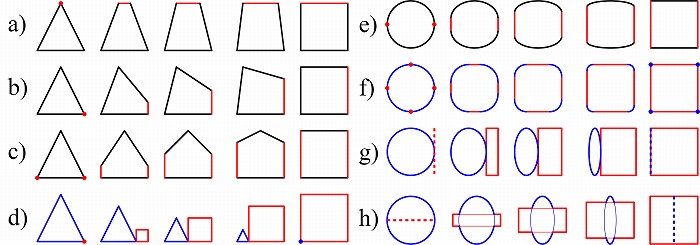
図9. 生成または消滅により形状を統合する例。赤い点または線から要素が生成され、青い要素
は点か線へ消滅している
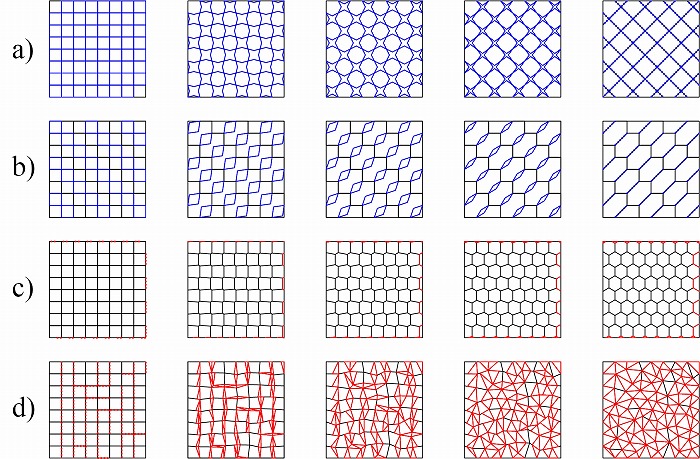
図10. 要素の生成または消滅によりパネル化アルゴリズムを統合した例
三つ目の要素の数を合わせる方法は、多すぎる要素を同じ要素に重ね合わせることで数を減ら
したり、同じ要素を複製して数を増やす方法である。図11aでは六角形の六つの辺のうち三つ
が重ね合わされて一つの辺となることで数が揃えられ、図11bでは三角形の辺の一つが複製さ
れて四角形の辺の数と揃えられ、図11cでは、分割と複製を組み合わせて部分的に重なり合う
四つの弧で構成して四角形の辺と数を合わせている。図11d~fは、領域の全体または部分的な
重ね合わせや複製により統合する領域の数を揃えている例である。
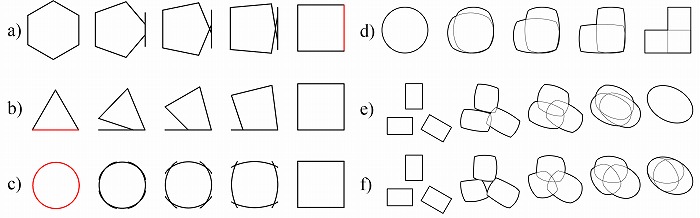
図11. 要素の重ね合わせまたは複製により要素数を揃える例
以上に見られるように、二つの形状を統合するには様々な方法があり、形状を統合するアルゴ
リズムを設計するときには要素の対応を積極的に考えることが重要である。そしてそこには色
々な設計の可能性が潜んでいるように思われ、筆者にとってその興味は尽きないのである(図
12)。

図12. 筆者が形状の統合を利用してファサード設計を行ったMorphosisによるエマーソン大学
ロサンゼルス校の中庭と、コーネル大学ゲイツホール(エマーソン大学ロサンゼルス校
写真撮影:渡辺太陽)