2024.12.19

パラメトリック・ボイス

　　　　　　　　　      コンピュテーショナルデザインスタジオATLV　杉原　聡

　 図1. M. C.エッシャー、メタモルフォーシスIII（1967-1968年）
　 ※上記の画像、キャプションをクリックすると画像の出典元のWikiArt.orgのWebサイトへ
　　 リンクします。

以前のコラムでも、設計の参考として挙げたが、筆者はM. C. エッシャー（図1）が好きであ
る。小学校か中学校で不思議な絵として紹介されて出会い、図書館でよく画集を眺めていたが、
その私への影響はモーフォシス在籍時に設計したコーネル大学ゲイツホールのファサードなど
の作品にも表れているように思われる（図2）。

　図2．モーフォシス、コーネル大学ゲイツホール（ファサード設計、写真撮影：筆者）

エッシャーの作品は、その絵の不思議さ、錯視効果、不可能幾何学がよく注目され、ちょうど
最近第3作が公開されたMonument Valley でも、その不可能幾何学を効果的に用いて迷路ゲー
ムが構成されている（不可能幾何学だけでなく、動的に変形する形態と空間の可能性も追求さ
れているので建築関係者に好きな方も多いかと思う）。

余談ながら、不可能幾何学の表現しやすさとも関連した、アイソメトリックと独特のシェーディ
ングを用いたMonument Valleyの表現スタイルは建築プレゼンテーションのスタイルの一つと
して参考になり、第1作が公開された2014年頃、当時南カリフォルニア大学で教えていた
Jose SanchezにMonument Valleyが如何に素晴らしいかよく聞かされた。そして彼はそれと
シムシティを融合したような都市デザインゲームBlock’hoodの開発を、2014年に香港で開催さ
れたSmart Geometryワークショップにて始め、筆者もそこで共同講師としてゲームのプレイ
ヤーがデザインした都市に住み、その出来を評価するNPCエージェント達を実装した。その後
それを商用ゲームとして開発しなおした話は、彼が登壇した建築情報学会チャンネル（クリッ
クするとYouTubeへリンクします）にて披露されている。

上記のように不可能幾何学の不思議さが注目されるエッシャーであるが、図1のように幾何学
パターンが変形しながら繰り返されるテセレーション作品も多く制作されている。これらのよ
うな作品を描くに至ったエッシャーの経緯を以下に辿ってみようと思う。

19世紀末のオランダに生まれたマウリッツ・コルネリス・エッシャーは、始めは建築を勉強し
ていたが上手くいかず、グラフィックアートに転科して絵画と版画を学んだ*1。卒業後、人
物、自然を描いた作品も多く制作していたが、スペイン、グラナダのアルハンブラ宮殿へ訪れ
て以来（1922年と1936年に二回訪れている）、そのイスラム装飾のアラベスクのような幾何
学模様に強く興味を持つようになった（図3）。

　 図3．M. C. エッシャー、アルハンブラ宮殿のモザイク（1922年）
　 ※上記の画像、キャプションをクリックすると画像の出典元のWikiArt.orgのWebサイトへ
　　 リンクします。

アルハンブラ宮殿で模写した様々なパターンの仕組みを研究するエッシャーに、地質学者で
あった兄のベレンド・ゲオルギ・エッシャーは、数学者ジョージ・ポリアや結晶学者
フリードリヒ・ハーグの論文を勧めた。これによりエッシャーは、結晶の格子構造や、数学に
おけるテセレーションの知識を深め（図4）、1936年以降、これらの知識を応用して、図１の
ような、ある形状が隙間や重なりなく平面を覆うテセレーション作品を多く制作するように
なったのである。

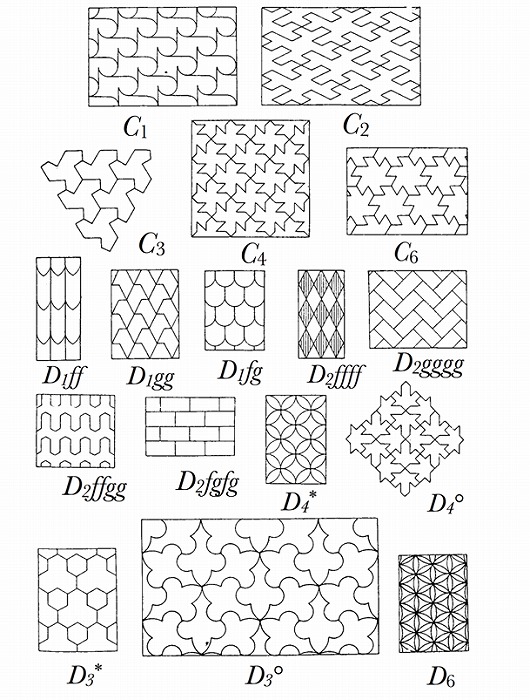
　　　 図4. ジョージ・ポリアによる17の文様群 *2（出典 *3）

1954年にオランダ、アムステルダムで開催された国際数学者会議に出席していたイギリス人
ノーベル賞受賞物理学者・数学者ロジャー・ペンローズと、同じくイギリス人数学者ハロルド・
スコット・マクドナルド・コクセターは、オランダの数学者がアムステルダム市立美術館で企
画したエッシャーの展覧会を訪れ、エッシャーの作品に感銘を受けた。

ペンローズは特にエッシャーの「相対性」（図5）が印象に残り、この絵における重力は再現不
可能だが幾何学は再現可能であり、幾何学も再現が不可能なものは考えられるだろうかと思案
し、ペンローズの父で遺伝学者・数学者のライオネル・ペンローズと共に、ペンローズの三角
形やペンローズの階段を考案して（図6）1958年に論文を書き*4、その論文を後にエッシャー
に送ったと言う。また、ライオネル・ペンローズの弟で画家のローランド・ペンローズが友人
のパブロ・ピカソにペンローズの三角形を見せたところ、ライオネルとロジャーはキュビズム
の画家になるべきだったと述べたという。

　図5．M. C. エッシャー「相対性」（1953年）
　※上記の画像、キャプションをクリックすると画像の出典元のWikiArt.orgのWebサイトへ
　　リンクします。

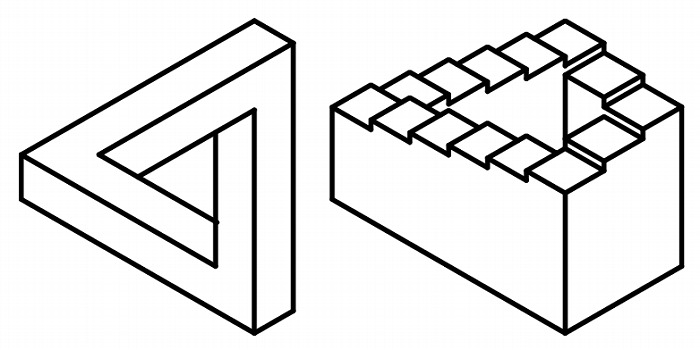
　図6．ペンローズの三角形と階段

それからしばらくしてペンローズの元にエッシャーから手紙が届き、ペンローズの階段に大変
な感銘を受けたので、オマージュとしてこの作品を捧げると、「上昇と下降」が送られてきた
と言う（図7）。

　　　　　 図7. M. C. エッシャー「上昇と下降」（1960年）
　 　　　　※上記の画像、キャプションをクリックすると画像の出典元のWikiArt.orgの
　　　　　　 Webサイトへリンクします。

また、ロジャー・ペンローズと同じくアムステルダム市立美術館でエッシャーの作品を見て感
銘を受けたコクセターは、自身の論文の挿絵にエッシャーの絵を使っても良いかエッシャーに
お願いし、快諾されたコクセターはその論文をエッシャーに送った。そしてその論文に含まれ
ていたポワンカレ円盤に感銘を受けたエッシャーは、それと同じ幾何学構造を持つ「円の極限I,
II, III」を制作した（図8）。

　図8. M. C. エッシャー「円の極限III」（1959）
　※上記の画像、キャプションをクリックすると画像の出典元のWikiArt.orgのWebサイトへ
　　リンクします。

このように、数学の専門教育を受けたことはなく、数学に苦手意識も持っていたエッシャーで
あるが、エッシャーは科学者との交流を持ちつつ作品を追求し、エッシャー自身の洞察力によっ
て、彼の作品には多くの科学的、数学的、幾何学的知見が内包される。

しかし、これらのようなエッシャー独自の作風はオランダ、ヨーロッパの画壇からは冷遇され、
一部の科学者以外からは注目されてこなかったエッシャーであるが、1960年代にアメリカの一
般向け科学雑誌Scientific Americanで作品が紹介されたり、またヒッピーのカウンターカル
チャーへ向けた雑誌Whole Earth Catalogでバックミンスター・フラーと並び紹介されてアメ
リカでの注目を受け始めた。レコードのアルバムカバーにエッシャーの絵が用いられることも増
えて大衆文化に浸透して言った一方、エッシャーの意図に反してその作品はヒッピー文化と連
動したサイケデリック・アートの一種との認識が広まってしまった。1969年に、ローリング・
ストーンズのミック・ジャガーがアルバムのカバー・デザインを依頼する手紙をエッシャーに
送ったところ、その不遜な文体を快く思わず、エッシャーは断りの手紙を送ったという。

1962年にロジャー・ペンローズがエッシャーの家を訪れたとき、ペンローズは自身が考案した
木のパズルをエッシャーに渡した（図9）。一つの形を繰り返して平面を充填するものであり、
敷き詰め方は一種類しか無いという。エッシャーはペンローズに宛てた手紙の中で見事に正解
を示しただけでなく、後年そのパズルに基づいた絵を制作した（図10）。これは、水彩による
テセレーションのエッシャー最後の作品となった。

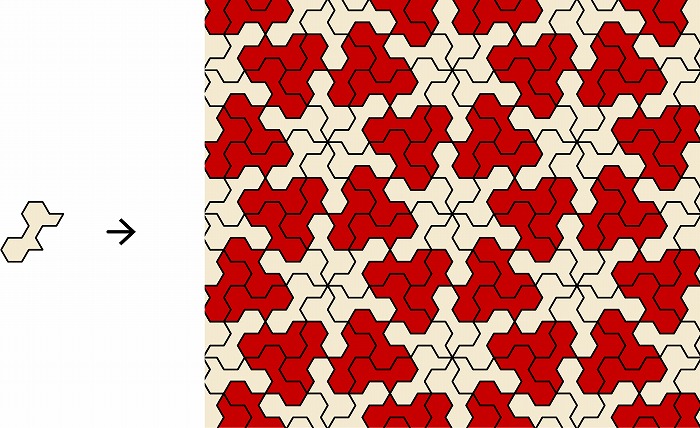
　図9. ペンローズによる平面充填パズル（赤いピースは白いピースを左右反転したもの）

　　　　図10．M. C. エッシャー「おばけ」（1971年）*5

上記のパズルは、パズルのピースを組み合わせて行くと、ある時点で周期が表れて、一つの周期
のグループを平行移動して複製することで再現なく平面を埋めることができる。しかし、平行移
動できる周期が永遠に表れないようなピースの形は存在するかという問題に取り組み、1970年
代にペンローズが発見したのが、二種類の菱形からなるペンローズ・タイルである（図11a）。
また、さらにこれを一種類にできないかと取り組む問題はアインシュタイン問題と呼ばれ、永い
こと事解決されずにいたが、反転を許せば充填できるThe hatと呼ばれる形が昨年2023年に発
見され（図11b）*6、さらにその後まもなく反転もせずに充填できるSpectreと呼ばれる形が発
見された（図11c）*7。（なお、Spectreもフランス語でおばけを意味する）。

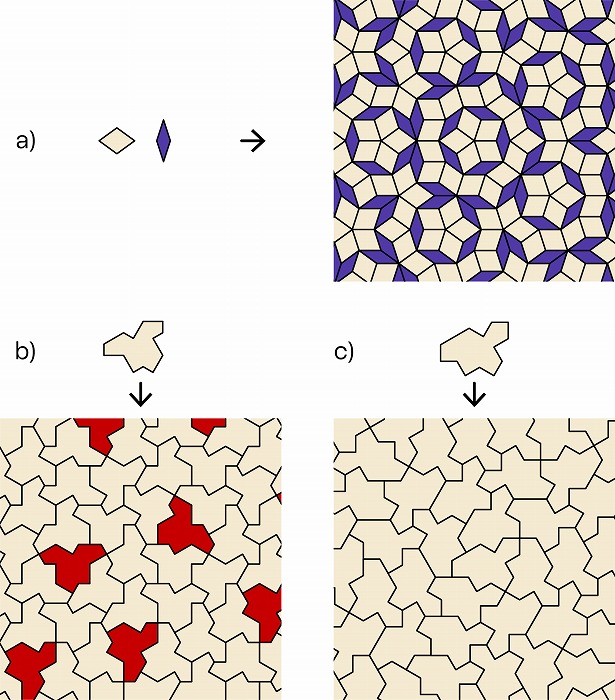
　図11. a)ペンローズ・タイルによる平面充填、b)The hatによる平面充填（赤いタイルは反転し
　　　　たもの）、c)Spectreによる平面充填

エッシャーは1972年に残念ながら他界したが、もし存命であったらペンローズ・タイルも、
The hatも、Spectreにも基づいた素晴らしい作品を描いたことであろう。

なお、エッシャーの最後の版画作品は1969年に制作された「蛇」であり（図12）、エッシャー
は最後に蛇の作品を制作することをかねてより決めていたという。図８の円の極限シリーズの
ように、円の外周に無限に小さくなる円が描かれるだけでなく、中心にも同様の極限が描かれ、
それと同時に図1や図7を含むエッシャーの多くの作品において表現される生ける者の終わりな
きループ、輪廻のような円環性も表現されているかのようである。これは、筆者には映画ネバー
エンディング・ストーリーの蛇の紋を思い起こさせると同時に、モーフォシスの建築家トム・
メインが、これは歴史上最高のドラマだと視聴翌日に熱く語っていたトゥルー・ディテクティ
ブのシーズン１で述べられた、時間は平らな円である、という謎めいた言葉とその元ネタであ
るニーチェも想起され、軽い身震いを覚える。

　　　　　図12. M. C. エッシャー「蛇」（1969年）
　　　　　※上記の画像、キャプションをクリックすると画像の出典元のWikiArt.orgの
　　　　　　Webサイトへリンクします。

これらのエッシャーが残した作品や、それと関連する数学、幾何学的知見の中には、まだまだ
建築設計の役に立ち掘り起こされるのを待っているものがあるように筆者には考えられ、
エッシャーへの興味は尽きない。

なお、このような興味から筆者はエッシャーの幾何学とNURBS立体（NURBS曲面を三次元に
拡張したもの）の分割による空間充填をテーマにした４日間のデザインワークショップ
「NURBS Volume Crystallography」を、2025年3月に東京大学で開催される国際学会
CAADRIA2025の中で行う予定であり、筆者の他にも9つのグループが多様なトピックの先進
的なワークショップを行う（使用言語は基本的に英語で、参加にはCAADRIA2025の参加登録
が必須となる）。参加者の募集は1月6日より先着順で開始するそうなので、世界から訪れる参
加者と共にデザインやファブリケーションに従事するのに興味のある方は是非ご参加を検討い
ただけたらと思う。

*1 Wikipedia - マウリッツ・エッシャー
*2 Wikipedia - 文様群
*3 Pólya, George. “Über die Analogie der Kristallsymmetrie in der Ebene.” Zeitschrift
　  für Kristallographie und Mineralogie, 60, 1924.
*4 Penrose, Lionel Sharples, and Roger Penrose. “Impossible Objects: A Special Type
　  of Visual Illusion”, British Journal of Psychology, 49, 1958.
*5 フジテレビギャラリー 編「M.C.エッシャー『遊びの宇宙』」小田急百貨店, 1983
*6 Smith, David, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss.
　  “An aperiodic monotile.” arXiv, 2023,
*7 Smith, David, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss.
　  “A chiral aperiodic monotile.” arXiv, 2023,

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
•