2025.02.27

パラメトリック・ボイス

　　　　　　　　　      コンピュテーショナルデザインスタジオATLV　杉原　聡

私が建築を学校で初めて学んだUCLAの建築修士1年1学期に、後年ハーバード大GSD建築学部
長を務めたマーク・リーが教えるスタジオ演習にて教科書に挙げられたのが、ピーター・アイ
ゼンマンの「Diagram Diaries」であった。修士制作の担当教官であると同時に卒業後最初に
務めた事務所がアイゼンマン事務所出身のグレッグ・リンであることも関係し、アイゼンマン
の言説はひどく難解であるものの、その数理・幾何学的な設計の側面のために個人的に好きな
建築家の一人である（好きすぎて、過去のコラムでも触れた"コンピュテーション現代建築史
のオンライン講義※クリックするとYouTubeへリンクします"にてアイゼンマンの話に時間を
割きすぎてしまったことがある）。

そのアイゼンマンの代表作の一つが、シンシナティ大学の建築学科の建物として1996年に竣
工したアロノフ・デザイン芸術センターである(図1)。竣工後の雨漏りで大学が施工業者を訴
えたり、コストを抑えた材料の老朽化による外装、内装の維持費などが問題になったりもする
が、数理的な幾何学操作による設計過程から生まれる多様性が筆者は好きで、後に勤務した
モーフォシスでは自分のデスクの壁に(よく考えるとトム・メインに失礼な話ではあるが)アロ
ノフ・デザイン芸術センターの平面図(図2)をずっと貼っていた。

　図1　ピーター・アイゼンマン「アロノフ・デザイン芸術センター」 (撮影: w_lemay)
　※上記の画像、キャプションをクリックすると画像の出典元のWikipediaのWebサイトへ
　　リンクします。

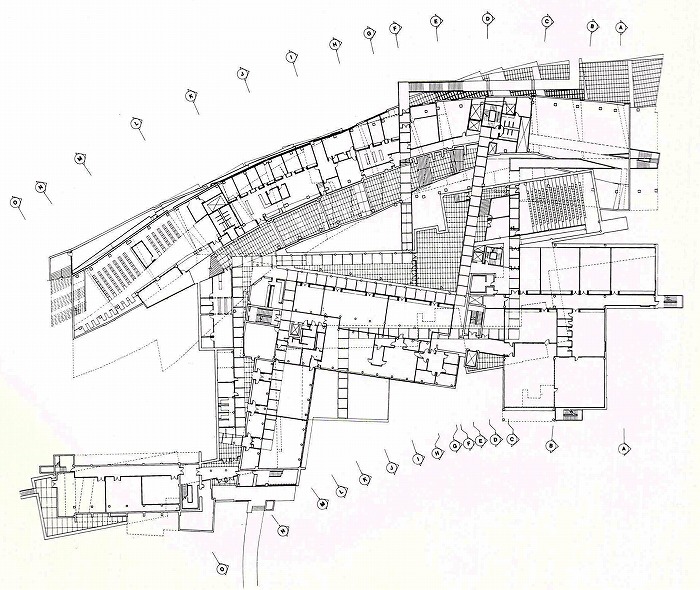
　図2　アロノフ・デザイン芸術センター平面図 (出展：Eisenman, Peter. Re-working
　　　　Eisenman. Wiley, 1993, 182.)

アロノフ・デザイン芸術センターの設計プロジェクトにリンと並んでプロジェクト・アーキテ
クトとして参加していたダナ・バリーの執筆した文章に、その設計過程の詳細が記されてい
る*1。その過程はコンピュテーショナルデザインにおけるルールに基づいた形態生成の観点か
ら見ても興味深く、バリーの文章を参考に、どのようにアルゴリズムのパラメータが増やされ
ていくかという視点から設計過程を以下に辿ってみる。

アロノフ・デザイン芸術センターは、丘陵地に建つデザイン・建築・芸術・計画学部の三つの
接続された既存の棟に建て増しされた増改築プロジェクトであり(図3)、設計過程は、増築で
追加する主なプログラムを収容する直方体を一列に並べるところから始められた(図4a)。そし
てまずそれらの直方体同士の重なりを考え、その重なる量を変化させている(図4b)。これはア
ルゴリズムとして考えると、直方体ごとに重なり量のパラメータを追加してその値を数値関数
の反復によって定めていることに相当する(用いられた数値関数は指数関数 y=1.6^x ={1.6,
2.56, 4.1, 6.55, 10.49, 16.78, 26.84, …}である)。
 

　図3　アロノフ・デザイン芸術センターの既存部(黒)と増築部(赤)

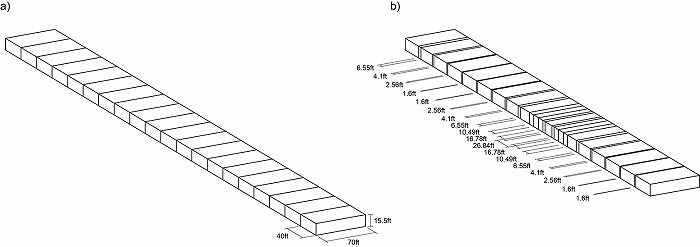
　図4　a) 直方体の列 b) 直方体の重なり

それから、隣接する直方体に対するXY平面上の回転角度パラメータを追加して、直方体の列
を曲線状に配置できるようにし、その角度の値を丘陵地である敷地の等高線に近くなるよう定
めている(図5a)。その後に主としてZ方向の変位ベクトルパラメータによって直方体の列を複
数の段に複製すると同時に、それぞれの直方体の短辺回りの回転変数を追加し、下段には小さ
な、上段には大きな角度を定めている(図5b)。そしてまた別の、主にY方向の変位ベクトルパ
ラメータによる複製を行い、もとの三段の直方体の列と重なり合う位置に、別の三段の直方体
の列が複製されている (図5c)。

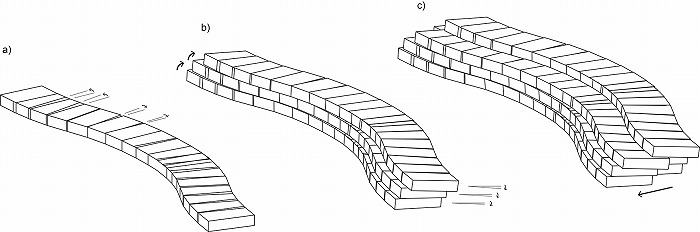
　図5　a) 直方体のXY平面回りの回転 b) 直方体のZ軸方向への複製と列の方向周りの回転
　　 　 c) Y軸方向への複製

それから図5aの曲線状に並ぶ直方体列に戻り、その直方体をZ方向に少しずつずらす変位パラ
メータを与えて、西に向かって階段状に上る勾配のある直方体の列を生成し、さらに回転角度
パラメータを与えてXY平面上で回転させている(図6)。

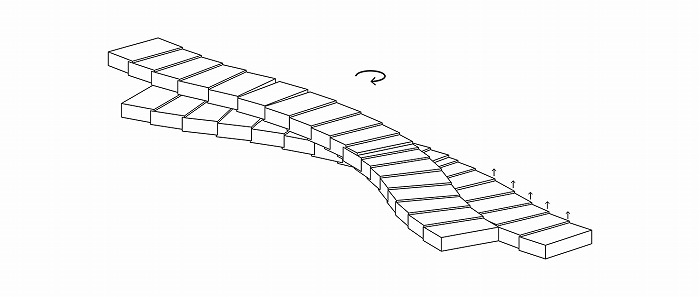
　図6　勾配を持つ直方体の列の複製とXY平面周りの回転

今度は既存の三つの棟のうち中央にある建物の廊下をトレースした、アイゼンマンがシェブロ
ンと呼ぶL字の形状を入力データとして読み込み、それを反復してジグザグ線のような形状を
生成する(図7a)。次に、この連続するシェブロンを複製、移動、回転し、中央の既存棟の廊下
と部分的に一致するシェブロンの他の部分が、左と右の既存棟の廊下または内壁とも一部一致
するようにその変位、回転パラメータが定められている。既存棟の輪郭もシェブロンと同様に
複製され、図7bのように複数のシェブロンと既存棟の輪郭が重ね合わされた。

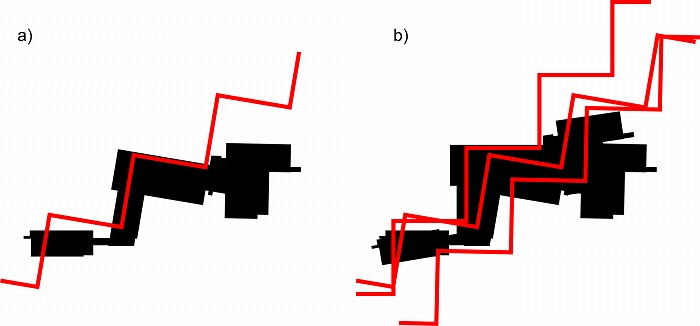
　図7　a)中央の既存棟の廊下形状に基づくシェブロン b) シェブロンの複製とそれに沿わせた
　　 　 既存棟の輪郭の複製

そして以上で生成された複数の形状は、次のようにまとめられて複雑な建物形態を構成する。
図5bの三段の直方体の列は、図5cの複製された三段の直方体の列を用いたブーリアン演算の差
によって吹き抜けのための空間が作られる。次に図6の勾配を持つ直方体の列が重ね合わせら
れ、東西方向に階を繋ぐスロープの通路が生成される。それから図7bのシェブロンが重ね合わ
され、各種ブーリアン演算により廊下や、吹き抜けを横切る橋が形成される。そして図7bの既
存棟の輪郭形状が重ね合わされて、建物の内部や外部の部分的な形状を定める。さらにシェブ
ロンは直方体の列を分断し、分断された各領域の直方体はXY平面上で変位が与えられてわずか
にずらされている。

このような幾何学操作の結果、図2の平面図や図8の模型に示されるような多様な形態を持つ建
物が設計された(竣工されたものはこの模型よりも主に外構部において単純化されている)。筆
者が昔建物を訪れたときには、平面図をずっと眺めていた割には動線を理解しておらず、東側
の正面入口から入って建物内部をなんとなく彷徨っていたら、気づくといつの間にか内装材と
雰囲気の異なる既存棟を歩いていて、建物内部の空間の連続性に驚いた。なお、冒頭に述べた
内装の劣化は少し気になり、訪れた日がどんよりと曇った日であったことや学生が余りいない
ときだったことも影響してか、空間の雰囲気にはあまり心地良さを感じなかった。しかし、そ
れを踏まえても前述のように数理的な幾何学操作から生まれる多様性の点で、今でも筆者の好
きな建物である。

　図8　アロノフ・デザイン芸術センター模型 (出展：*1 Barry, Donna. “Connecting the Dots:
　　 　 The Dimension of Wireframe.” In Eleven Authors in Search Of a Building,
　　 　 edited by Cynthia Davidson, The Monacelli Press, 1996, 102.)

なお、アロノフ・デザイン芸術センターにおいて、図4aから生まれて様々な操作を受けた直方
体の角が、建設された建物の内外装の随所に現れるように、アイゼンマンの設計した建物に現
れるインデックスと呼ばれる設計過程で建物に刻まれる痕跡は、建物自身がどのように設計さ
れたかを自己言及する重要な要素である。しかし一方で、その空間を体験する多くの人々はア
イゼンマンがそれをどのように設計したかなどはどうでもよいことである、との批判の声が挙
がることもある。

ではそもそも、アイゼンマンがダイアグラムを用いた数理・幾何学的な操作によって設計を行
うのは何故であろうか？その答えはアイゼンマンの難解な言説の中にあると思われるが、その
全体が未だ理解できていない私には、以下のような要因もそれらに加わるのではないかと思う。
 
アイゼンマンは講演でしばしば、ケンブリッジ大学の博士課程在学中に彼が教わった師である
コリン・ロウと二人で90日間かけてヨーロッパの建築物を旅して回ったエピソードを述べてい
る。夏の暑い日にイタリアの小さな町モンタニャーナを訪れ、そこで初めてパッラーディオの
作品を見たという(図9)。喉が乾いていたアイゼンマンにロウは「私はそこの店でビールを飲
んでいるから、君はあそこのパッラーディオのヴィラの前に立って、そのファサードについて、
目には見えないことを発見してから来い」と言ったという。アイゼンマンはファサードをつぶ
さに観察し、その要素の幾何学的関係や比率から考えられることをロウに言っても「それは見
えることだろう」と追い返され、アイゼンマンはヴィラの前で何時間も観察を続けたという。
最終的には、ヴィラの中心へ向かう力のようなものが感じられる、と言ってようやくビールに
ありつけた、といった話であったように思う (この点は筆者のうろ覚えである)。なお、アイ
ゼマンは後年パッラーディオの分析に取り組み、その成果は展覧会と書籍*2にまとめられてい
る。そこで、玄関前の空間であるポルチコを本来形成するはずの柱列、屋根、ペディメントな
どが、このヴィラでは壁面まで後退してファサードの一部となっており、それによって前面か
ら奥へ向かう動きと、壁面背後に室内とポルチコが混ざったような中間領域が生まれているこ
とが示されている。

このロウとの経験がアイゼンマンにとってかけがえのない建築の学びであったことが講演でよ
く述懐されており、アイゼンマンが数理・幾何学的な操作を用いる理由の一つは、このような
目には見えない建築の質を生み出そうとするためではないかと筆者は考える。ただ、そのよう
な操作によって質が生み出せたか否かはまた別の問題であることは留意しておく。

　図9　アンドレア・パッラーディオ「モンタニャーナのヴィラ・ピサーニ」(撮影: Hans A.
　　 　 Rosbach)
　※上記の画像、キャプションをクリックすると画像の出典元のWikipediaのWebサイトへ
　　リンクします。

以上のように、アイゼンマンの数理・幾何学的操作をコンピュテーショナルデザインにおける
パラメータの観点から見てきたが、アイゼンマン自身はパラメトリックデザインやBIM、コン
ピュテーショナルデザイン全般に批判的である。それは、それらにおけるパラメータの操作や
アルゴリズムの利用が、手に届く範囲にあって面白そうだからやってみた、というだけであり、
その設計に設計者の建築に対する問題意識と意図が感じられないものばかりであるからだと言
う。アイゼンマンが等しく批判する、面白そうな形だからしてみたや、面白そうな素材の組み
合わせだからやってみた、という悪い意味での現象学的な建築と同じだと言うのだ。

上述したアイゼンマンの数理・幾何学操作に意図が読み取れるかはこれまた別の問題な気はす
るが、少なくとも我々が設計をするときに、無自覚に設計操作を行っていないか、明確な意図
を持って設計に考慮すべきパラメータを導入しているか、またそもそも、そのように意図を持
つべきなのか、そしてそれは何故か、という点は引き続き自問を続けたいと思う。

*1  Barry, Donna. “Connecting the Dots: The Dimension of Wireframe.” In Eleven
　　Authors in Search Of a Building, edited by Cynthia Davidson, The Monacelli Press,
　　1996, 48-59.
*2   Eisenman, Peter and Matt Roman, Palladio Virtuel. Yale University Press, 2015.
 

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
•