![]()
設計の合理化~その3・ユニット化~
2020.08.27
パラメトリック・ボイス
今回は、設計の合理化について残る最後のトピックであるユニット化について述べる。
事後的ユニット化(Post-unitization)とユニットの構成による設計(Pre-unitization)
複雑な建築形態の合理的ファサード設計の典型的な手順では、まず形態の合理化を行った後、
合理的曲面分割を行い、分割された領域に配置された多種のファサード形状を限られた種類の
ユニットに落とし込む。ミラノ万博中国館の屋根ファサードの設計プロセスでは、前々回コラ
ム「設計の合理化~その1・形態合理化~」の図1で示したように形態合理化を行った後、
以下の図1のような形で曲面分割とユニット化を行った。
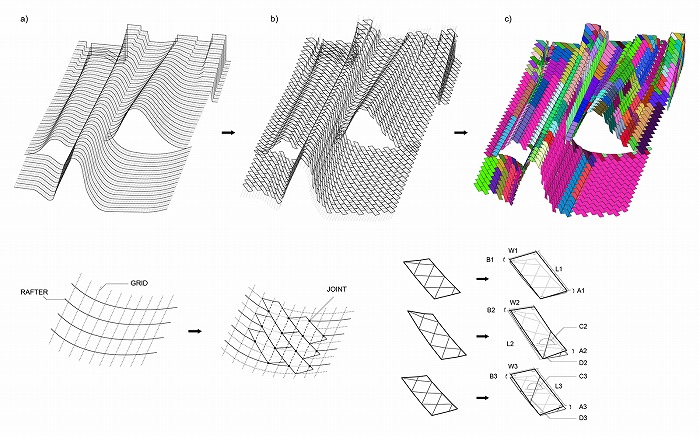
図1.ミラノ万博中国館の曲面分割とユニット化(建築設計:Studio Link-Arc、屋根ファサー
ド設計:ATLV)
合理化された屋根の曲面は、図1aのようにできるだけ形態の稜線と一致し均等に分割された
内部グリッドを構成し、それから図1bのように曲げを含む斜めのパネル領域に隙間なく分割
された。そして各々のパネル形状はその曲がり具合に応じて折曲げ数は最大2つに抑えられ、
展開形状は限られた種類の矩形に近似された。このようにしてパネル・ユニットの種類を抑え
て同一ユニットをできるだけ繰返せるようにして効率化が試みられた。
なお、このようなパネル形状の近似によるユニット化が容易に行えるのは、パネル間の隙間や
重なりがある範囲で許される場合であり、パネル同士がぴったり隣接しなければならないとき
のように許容範囲が狭い場合には困難となる。
上記の例は一旦生成された多くの種類のパネル形状を限られた種類のユニットに落とし込む事
後的な合理化手法であるが、逆に限られた種類のユニットを予め設計してそれらの組み合わせ
によって設計を行う方法も合理的な設計手法の一つと言える。パネル・ユニットから設計を始
める例として以下にコーネル大学ゲイツホールのファサードを挙げる(図2)。このプロジェ
クトでは限られた種類の日除けのパネルで建物を覆い、疎密の変化と形状の方向性で動きを与
えつつ、図と地の反転を意識した形状で部材と空隙がうまく組み合う構成となるようにパネル・
ユニットの設計を試みた(図3)。

図2.コーネル大学ゲイツホール(建築設計:Morphosis、ファサード設計:杉原聡)
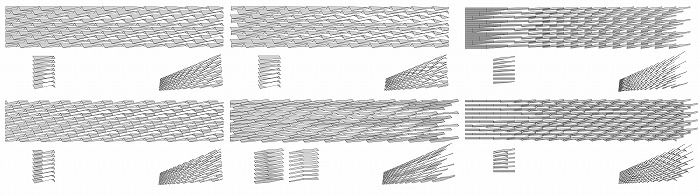
図3.コーネル大学ゲイツホール、ファサード設計スタディ
図4のイスタンブール都市博物館のファサード設計の例では、パネル・ユニットの種類と同時
に平面分割のためのグリッド形状も様々に検討し、パネルを支える構造の合理性や建築形態と
の整合性を考慮してグリッド形状とそれに応じたパネル・ユニットが設計された。

図4.イスタンブール都市博物館(建築設計、パース画像:Salon Architects、ファサード
設計:ATLV)
なお、矩形/三角形/六角形などのパネルの分割領域を積極的に表現するのではなく、面全体を
連続的に表現するために組み合う形状を持つパネルや、隣接パネル同士で模様が連なるような
パネル・ユニットの設計には、結晶学の知見に基づくMCエッシャーの平面充填(テセレーショ
ン)作品が良い参考となる。
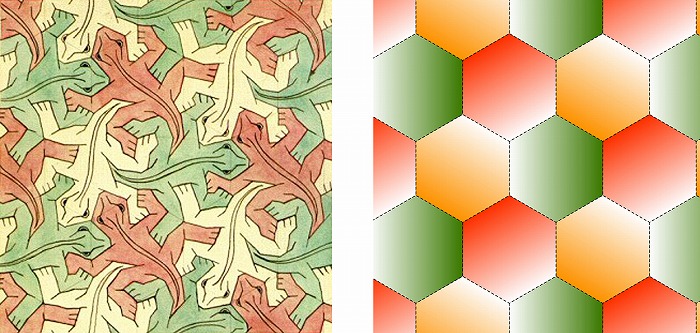
図5.MCエッシャーによる平面充填(左図はWikipediaより引用)
※上記の画像、キャプションをクリックすると画像の出典元のWikipediaへリンクします。
パネルの製造のための合理化
以前のコラム「制約を設計のチャンスに変えるアジリティと柔軟性」でも紹介したが、エマー
ソン大学ロサンゼルス校の中庭ファサード(図6)の設計プロセスではコンピュテーションによ
り流動的で連続的なファサード・パネルを生成した後に事後的ユニット化を行っている。アル
ミ板の折曲げで製造されるパネル・ユニットは、単に元の多種の形状を限られた種類の形状に
落とし込むだけでなく、更に製造の制約と効率を考慮した形状に合理化された。パネルの展開
形状はぴったりとアメリカでの標準寸法4フィート×8フィートのアルミ板に収まる8種類の平
面形状にユニット化され、パネルの3次元形状はそれらを折曲げてできる15種類の形状(反転
形状を含む)にユニット化された(図7)。

図6.エマーソン大学ロサンゼルス校中庭ファサード(建築設計:Morphosis、中庭ファサード
設計:杉原聡)
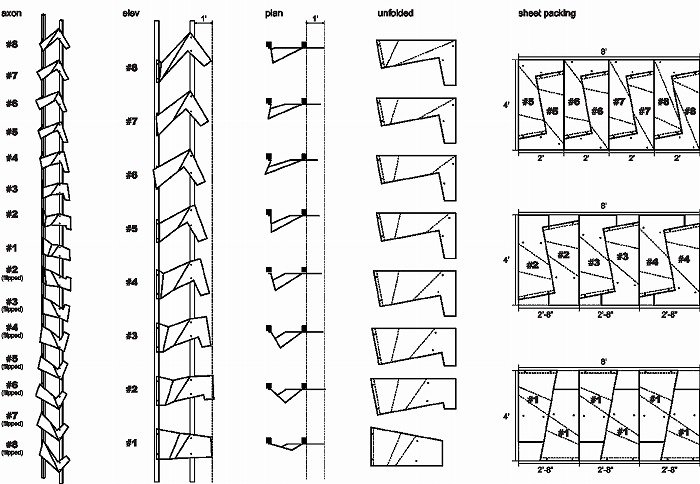
図7.エマーソン大学ロサンゼルス校中庭ファサードのユニット
またその一方で、類似した手法による合理的形状のパネル・ユニットの設計からスタートし、
ユニットの配置を後から設計したのが図8の内装プロジェクトである。まず6つの展開形状を
6種類の折曲げ方で36種類の3次元形状のパネル・ユニットが設計された。そしてパネル・ユ
ニットが配置されるのは図9の左に示される不定形な天井曲面上の、平面とは限らない四角形
領域であり、どの種類のパネルをどこに配置するかが問題となる。これには全探索アルゴリズ
ムを用いて、各領域内に収まり、なおかつ被覆面積が最大となる最適なパネル・ユニットの種
と微調整位置、微調整角度を割り出した。

図8.クライド・フレイジャーズ・ワイン&ダイン(内装設計:Morphosis、天井ファサード
設計:杉原聡)

図9.パネル・ユニットが配置される天井の形状と最適パネル探索アルゴリズム
ファサード構成の連続性とパネル・ユニットの種類
事後的にユニット化は、元の多数の種類のパネルを限られた種類に減らす。そのようにして合
理性を得る一方で、パネル構成全体におけるパネルの遷移の滑らかさは失われることが多い。
パネル・ユニットの設計から始める場合であっても、ユニットの種類が多ければ滑らかで連続
的な遷移が可能であるが、少なければパネルの種類が変化するときの差異が目立ち、粗い遷移
となる(図10)。それではユニットの種類の数はいくつが最適であるか?これは設計者に
とって、特にユニットの種類をパラメーターで制御しているコンピュテーショナル・デザイナー
にとって重要な問題であるが、これは設計者にとってのみの問題ではなく、その構成による設
計や表現が多方面に与える価値と、その実現に掛かるコストを踏まえた、プロジェクトのス
テークホルダー全員にとっての問題である。設計者にとって重要なことは、あり得る選択肢の
提示とその評価など、適切な意思決定に必要な判断材料を提供することであると筆者は考える。

図10.パネル・ユニットの種類の数と構成表現の連続性
以上3回の連載にわたり、設計の合理化、特にファサード設計における合理化の事例について
記した。基礎的な幾何学知見を用いた手法は今後も大きく変わるものではないが、製造や施工
のコストの掛かり方は、素材や工法、業者によりケースバイケースであり、なおかつ製造・建
設技術の進歩によって求められる合理性も変わってゆくため、今後とも様々な設計の合理化手
法が編出されてゆくことが期待される。



























