![]()
設計の合理化~その1・形態合理化~
2020.04.23
パラメトリック・ボイス
コンピュテーショナルデザインは複雑な形態や部材の組合せの設計を可能にするが、そのまま
ではその複雑性が建設・施工のコストの増大に繋がるため、それを抑えるために設計の合理化
を行うことが多い。合理化には、建築形態の合理化、合理的曲面分割、部材のユニット化、部
材形状の合理化といった種類が挙げられる。またそれぞれの合理化を行うタイミングには、設
計を考案する過程で合理性を考慮する場合(pre-rationalization)と、設計が一度決まった後に
行う場合(post-rationalization)がある。今回のコラムではまず形態の合理化に焦点を合わせて
その方法と例を記す。
平面、円柱・円錐面による形態合理化
形態の合理化は、後の工程での構造やパネルのための合理的分割、並びにユニット化を容易に
するために、建築形態の全体や部分を合理的な形状にすることである。基礎的な方法は、形態
を構成する面を平面と円柱・円錐面で近似することであり、構造や平面計画のためのグリッド
を効率的に構成できるように直線や平行線を面上や面の境界に増やすこともある。
例として、ミラノ万博中国館の形態合理化を図1に示す。建築形態は南立面を中国の山麓、北
立面を都市部をイメージした輪郭線を繋いだものとなっている。コンペの段階では限られた時
間の中でのアイデア実現のために合理化はせず、ラフな形状のままファサードを生成したが、
本案がコンペで選ばれて実施設計に入った段階で著者がファサードの合理性と効率的な構造グ
リッドの形成のために形態合理化を行った。初期の形態では矩形の敷地の長手方向に稜線が
走っているものの、並行でなくわずかに曲がった線が多くあったため、まずそれらを並行な直
線にし、特に中央の尾根の両脇の線を建物全体の構造グリッドの基準線として用いることを提
言した。そして2m間隔で短手方向のグリッド線を構成し、曲面の南北の端をできるだけグリッ
ド線上に合わせた。また曲面の境界線は直線と円弧で再構成した。なお北立面の直線的な断面
は南側の曲面に比べて複雑であり、曲線断面から直線断面への遷移は合理化困難な領域を生み
出すため、遷移領域を無理のない範囲で縮めて北側に寄せた。
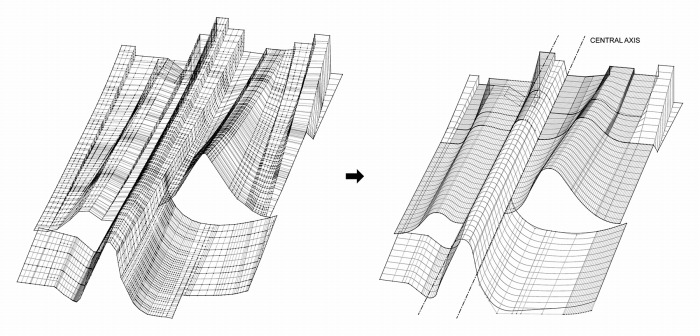
図1.ミラノ万博中国館の形態合理化(設計:Studio Link-Arc、屋根ファサード設計:ATLV)
上記の例は建築形態決定後に合理化を行ったpost-rationalizationの例であるが、合理性を確保するために平面、円柱面を組合せて形態を設計するpre-rationalizationの例を次に示す。図2
に示したファール・タワーの形態は、直方体を平面の組合せで切り出し、角をフィレットで丸
めることでモデリングされている。そのため形態は、円柱面の縁(橙線)を更にフィレットし
た複曲面(水色)は多少あるものの、大半は合理的な平面と、直線(紫線)をフィレットした
円柱面(青色)で構成されている。但しこのような形態が生成されたのは合理性を強く意図し
て設計されたからではなく、事務所が使用していたBentley Microstationが当時ソリッド向き
のモデラーであり、自由曲面のモデリングが困難であったことから、曲面形態を生み出すのに
多面体を段階的にフィレットする手法を設計者が編出したためである。これは、制約のある合
理的なツールを創造的に利用することによって、創造的ながらも合理性のある設計が可能とな
る例と言える。なおフィレットで生成された形状はガラスパネルのための曲面分割に生かされ
たが、詳細は次回に譲る。
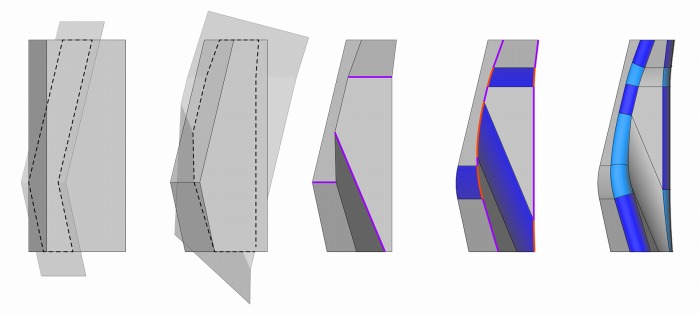
図2.ファール・タワーの形態生成過程(設計:Morphosis )
平面、円柱・円錐面以外にも図3に示すように、a.押出し曲面(extrusion)、b.回転曲面、
c.トランスレーショナル曲面、d. 線織面(ruled surface)、e. 可展面(developable surface)と
言った、各々何らかの合理性を持つ曲面の種類がある。
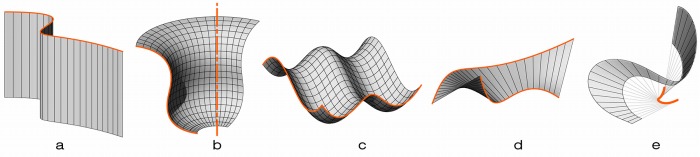
図3.5種類の合理的な曲面
押出し曲面は曲線を直線的に押出した曲面であり、押出し方向への規則的なパネル分割や、直線部材の当てはめができる。回転曲面は軸回りに曲線を回転させた曲面であり、回転対称性が
あるため回転方向に同一形状に曲面分割できる。トランスレーショナル曲面は一つの曲線をも
う一つの曲線に沿わせて形成される曲面であり、曲面分割で同一形状パネルの繰返しは必ずし
も可能ではないが、曲面を三角形ではなく平らな四角形で分割・構成できる。線織面は連なる
直線によって形成される曲面であり、常にある方向に直線部材を当てはめられるが、平らな四
角形で分割・構成可能とは限らない。しかし線織面の一種で連なる直線にねじれが無いものは
可展面と呼ばれ、その線に沿って平らな四角形で分割・構成可能である。しかも曲面全体の厳
密な平面展開が可能であり、一方向への曲げが容易な板金材などで建設が可能になる。複雑な
曲面で構成されるフランク・ゲーリーの建物の曲面ファサードは、設計後に可展面に合理化さ
れ、板金材で建設されることが多い。但し可展面への合理化が無理なく行える理由は、ゲーリー
事務所での設計過程が模型を多用し、紙や布といったシート材で構成した模型の検討を通じて
建築形態が形成されることが多く、模型を構成するシート材の物理的合理性を、建築形態が継
承しているためである。

図4.ホテル・マルケス・デ・リスカル(設計:フランク・ゲーリー、撮影:著者)
自由曲面の四角形パネル化これまでに挙げた曲面を超える不規則性を持つ自由曲面には、合理化の普遍的な手法は存在せ
ず、するとしても曲面の特徴を個別に観察して全体または部分に上記いずれかの合理的曲面に
近似することとなる。また曲面分割をして平面パネルで構成する場合、どのような自由曲面で
も三角形のパネルであれば隙間なく分割・構成できるが、平らな四角形のみの厳密な分割は
一般的に困難である。任意の自由曲面を平らな四角形のみで分割する方法は、四角形パネル化(quadrilateral panelization)または平面四角形メッシュ(planar quadrilateral mesh)問題と
して幾何学研究で取り組まれており、現在はMITでSelf-Assembly Labを主宰するスカイラー・
ティビッツが図5のインスタレーションで取り組んだように、またはマイクロソフト研究所の
ヤン・リウらが提案した、曲面をオフセットしても四角形の平面性が失われない合理的曲面
(図6)のように、ある条件や合理性または近似精度での四角形パネル化手法が研究・開発さ
れている。今後より汎用な自由曲面の四角形パネル化手法が開発されることが期待される。

図5.Tesselion: Adaptive Quadrilateral Flat Panelization ©SJET(設計:スカイラー・
ティビッツ)
※上記の画像、キャプションをクリックすると画像の出典元のTesselionのWebサイトへリンク
します。

図6 “Geometric Modeling with Conical Meshes and Developable Surfaces”
© Liu, Pottmann, Wallner, Yang, Wang ヤン・リウのウェブサイトより抜粋。右図の設計
はB. Schneiderによる。
※上記の画像、キャプションをクリックすると画像の出典元のYang Liu氏のGitHub Pagesへ
リンクします。リンク先で同じタイトルのテキストをクリックすると、上記の画像のページ
が表示されます。
よる新しいものでは必ずしもなく、ル・コルビュジエとクセナキスのフィリップス館の線織面
やウツソンのシドニー・オペラハウスの球面近似のように過去から引継がれる建築の知見であ
るが、近年のデジタル・ツールの発展と前回のコラムでも述べたコンピュテーショナルな手法
の俊敏性と柔軟性から、合理化手法の適用が活発になっている。今回のコラムでは設計の合理
化の中でも特に形態合理化について述べたが、次回は合理的曲面分割と部材のユニット化につ
いて述べたく思う。