![]()
コンピュテーショナル・デザインにおける
連続性と離散性~その2~
2022.11.17
パラメトリック・ボイス
コンピュテーショナルデザインスタジオATLV 杉原 聡今回のコラムでは、前回に引き続き連続と離散について記すが、特に連続性と離散性の種類や、
連続性の離散化と離散性の連続化について考える。
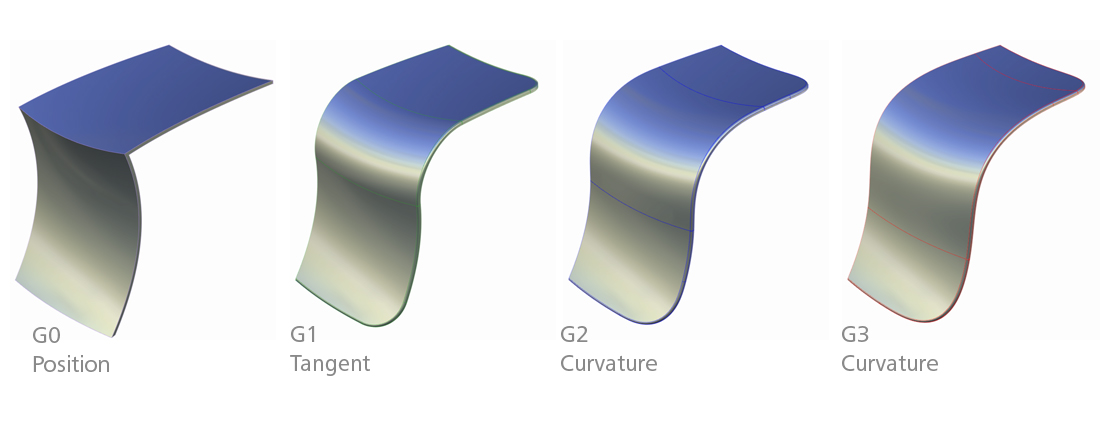
図1. G0, G1, G2, G3連続性
※上記の画像、キャプションをクリックすると画像の出典元のAutodeskの
Webサイトへリンクします。
曲面モデリングにおいて、連続性の種類としてG0, G1, G2, G3がある(図1)。G0は曲面の位
置は連続しているが法線方向は断続している状態、G1は法線方向は連続して変化しているが
曲率(法線方向の変化率)は断続、G2は曲率が連続しているが曲率の変化率が断絶、G3は曲率
の変化率も連続している状態である。これらは数理的に定義される滑らかさの違いであるが、
連続性にも色々なレベルがあることを示す。
また連続性の種類として、一つの方向に連続的である一次元的なもの(図2)や、複曲面のよう
な二つの方向に連続的な二次元的な連続性(図3)、ボリューム内の密度や状態のような三次元
的なもの(図4)と、異なる連続性が考えられる。

図2.一次元的連続性、グレッグ・リン「Stranded Sears Tower」
※上記の画像、キャプションをクリックすると画像の出典元の
GREG LYNN FORMのWebサイトへリンクします。

図3.二次元的連続性、グレッグ・リン「Embryological House」
※上記の画像、キャプションをクリックすると画像の出典元のCanadian Centre for
ArchitectureのWebサイトへリンクします。
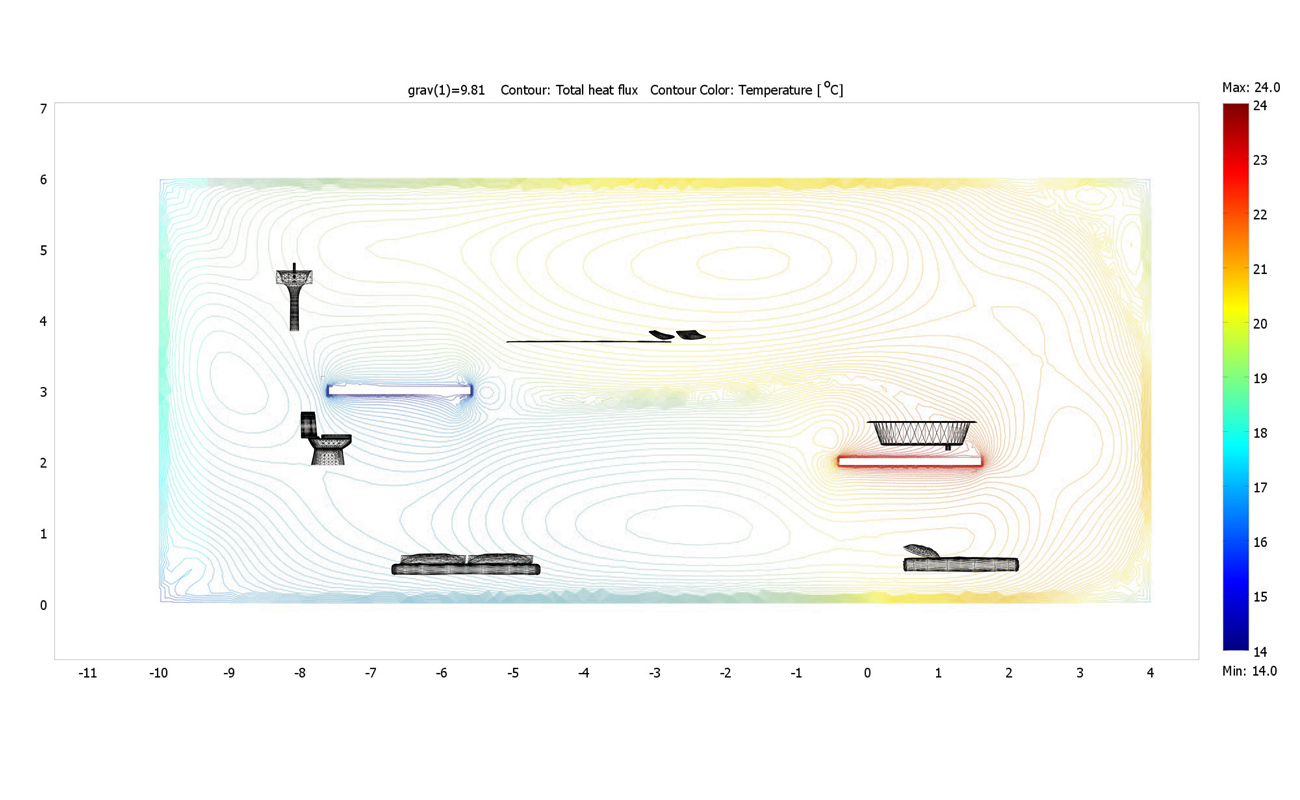
図4.三次元的連続性、フィリップ・ラム「Interior Gulf Stream」
※上記の画像、キャプションをクリックすると画像の出典元のPhilippe Rahm architectesの
Webサイトへリンクします。
また離散的なものの種類には、連続的なものと対応関係にあるものと、そうでないものがある。
整数は連続的な実数を離散化したものと見られるし、離散的ピクセルが並ぶラスター画像と連
続的なベクトル画像、ボクセルモデルとNURBSモデルも同様の関係にある。それらの離散性
は、対応する連続的なものと同様に近傍や順序を考えられるが、それができない離散的なもの
もある。
例えば、りんご、みかん、いちごと言ったフルーツの集合など、集合論で扱うような数値的で
ない要素のように、近傍や順序を定義することが困難なものがある。部材の材質や、BIMオブ
ジェクト属性で扱うような柱、壁、窓というような種類の情報も、この種の離散的な情報であ
ると考えられる。また、サヴェリオ・ムラトーリやクリストファー・アレグザンダーが示した
ようなタイポロジー(図5)もこの様な種類の離散的情報と考えられる。トーラスやクラインの
壺など連続性のイメージが強いトポロジーにおいても、穴の数や面の裏返り方などのタイプは
離散的な情報であり、1つの穴のある形状と2つの穴の中間の1.5個の穴というものは考えられ
ない。結び目理論において考えられる結び目のタイプも離散的な情報である。
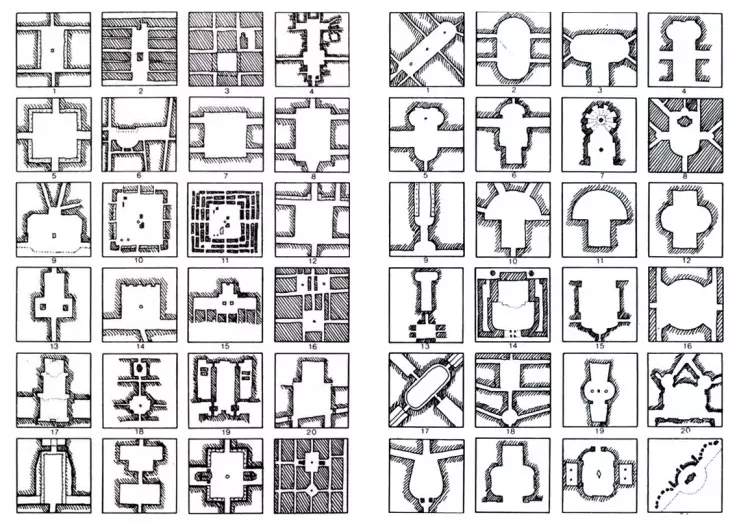
図5.クリストファー・アレグザンダーによるタイポロジー例
※上記の画像、キャプションをクリックすると画像の出典元のndionのWebサイトへ
リンクします。
次に連続性の離散化について考える。アナログ信号からデジタル信号への変換での時間軸方向
での標本化と、信号値を離散値にする量子化は連続的な情報の離散化の例と言える。また、
NURBS曲面やそれらによるソリッドモデルをボクセルモデルに変換するプロセスや、曲面を
離散的なパネルに変換するパネル化(図6)もそれに類する離散化の手続きと言え、離散化され
た要素郡は手続き前の連続性を内包する。ディスクリート派と呼ばれるジル・レツィンらが近
年主張する、建設の合理性を踏まえ、デジタル建築以降続く連続性の建築を乗り越えようとす
る設計手法で示される離散化も似た側面を持つ(但し連続的形態の離散化を行わないモジュー
ルのボトムアップな集積で設計する場合もある)(図7左)。また、このような離散化ではどの程
度の解像度で行うかによって離散性の度合いが異なる。細かい離散要素によって高解像度で離
散化されたものは、高い連続性を維持するが、粗い離散要素により低解像度で離散化されたも
のは、元の連続性が大きく失われて離散性が高まり、離散要素各々の主張が強くなる(図7右)。

図6.曲面のパネル化例、ザハ・ハディド建築事務所「Nordpark Railway Station」
※上記の画像、キャプションをクリックすると画像の出典元のZaha Hadid Architectsの
Webサイトへリンクします。
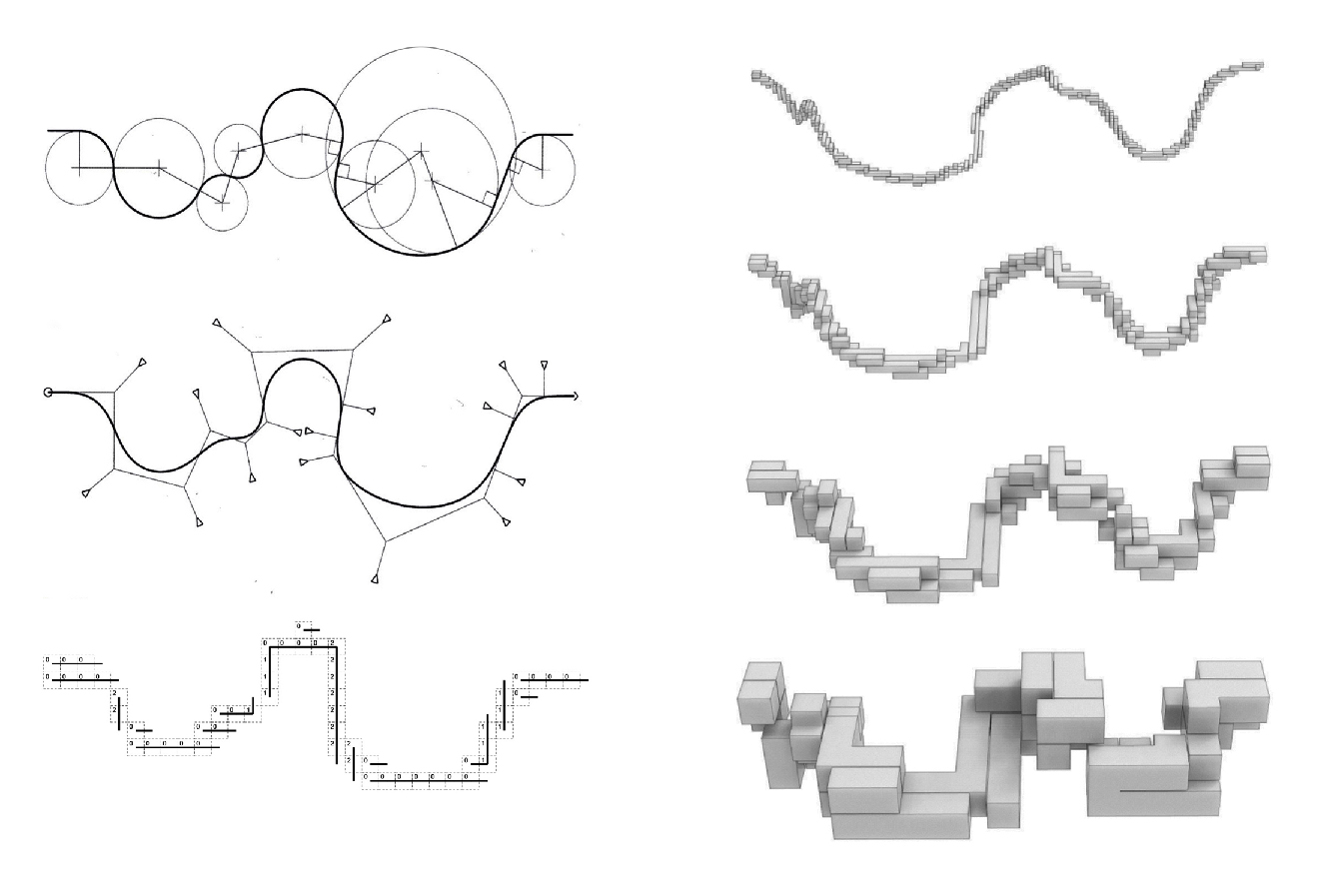
図7.連続性のデジタル建築に対抗するディスクリート派の設計アプローチ図(左)と
離散モジュールの解像度(右)
※上記の画像、キャプションをクリックすると画像の出典元のWebサイト(PDF)へリンクします。
また逆に、離散的なものの連続化を考える。概念的には、離散性は要素の関係の無さに表れる
と言えるので、要素の間に何らかの関係性が見えるとき、連続性が表れる。近傍にあるだけで
なく、列に並んだり、漸次的な変化で関係が表れることもあれば、要素がお互いに適応して関
係性が築かれ連続化されることもある(図8)。図9はパネルで構成されるファサードにおいて
その様な連続性が表れる例である。また、粗いポリゴン・メッシュの3Dモデルをメッシュの
面の再帰的な分割により滑らかにするサブディビジョンも、連続化の一種と考えられる。
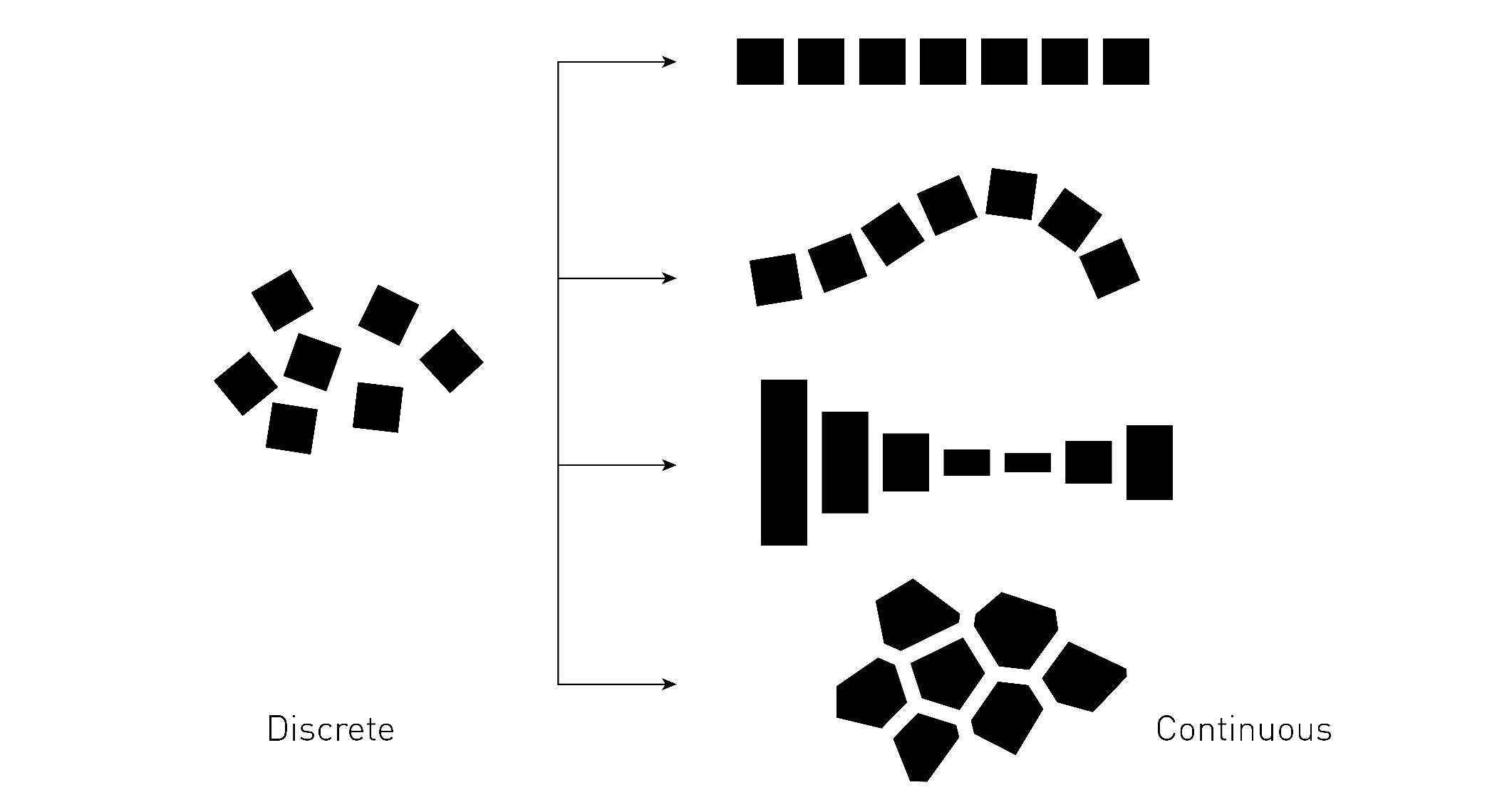
図8.離散の連続化

図9.筆者設計によるコーネル大学ゲイツホールとエマーソン大学LA校のファサード(建築
設計:モーフォシス、写真右:渡辺太陽)
最後に、コンピュテーショナル・デザインにおいてエージェント・シミュレーションを用いる
ときの連続性と離散性について述べる。エージェント・シミュレーションで生まれる情報の何
に着目してどのように利用するかは自明ではなく、設計者がその都度考えなければならない。
空間を遊泳するスウォーム・エージェントは通常その滑らかな動きの軌跡に着目され、それが
形態生成に利用されがちであるが、ある時点におけるエージェントの位置分布に着目すると、
エージェント達はルールに則して最適な分布状態を達成しようとしている(図10)。なので、
軌跡に着目すると連続性が強調され、エージェントの位置分布に着目すると離散性が強調され
る結果となる。また、軌跡自体を動的なエージェントと考えると、連続的な形状をもつ離散要
素として捉えることもできる(図11)。枝分岐エージェントのシミュレーションでは、枝の成
長を見ると連続的なものに見えるが、ある時点で生成された枝先のエージェントを見ると、離
散的な分布としても見られる(図12)。更に軌跡を副次的な情報として見ると、離散要素のだ
れがどこから分岐したかという兄弟/親子関係が表れる。このようにエージェント・シミュ
レーションでは、連続する時間軸で見ると連続性が強く見られ、空間で見ると離散性が見られ
る傾向があり、その着目点やバランスを決定するのは設計者である。
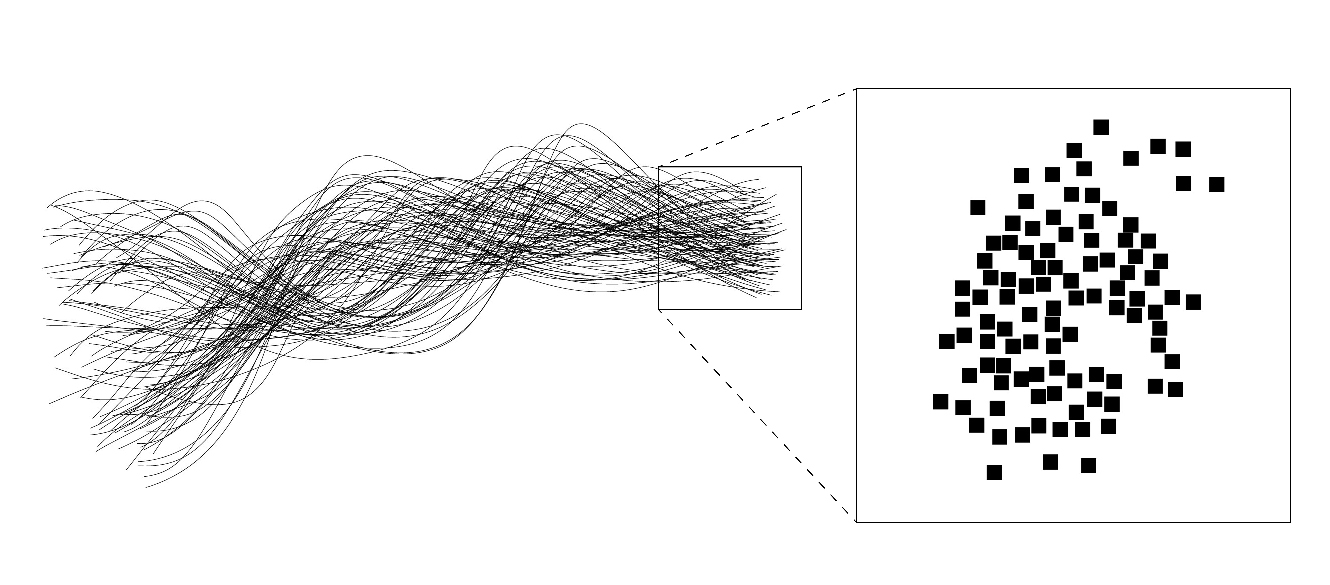
図10.スウォーム・エージェントの連続性と離散性
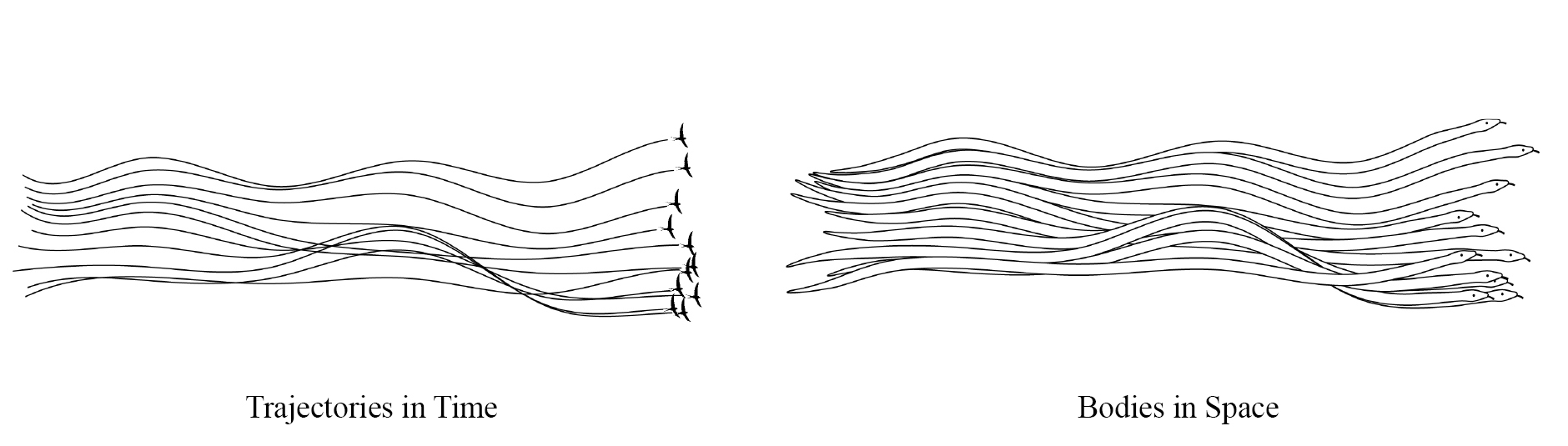
図11.時間における軌跡と空間における実体

図12.枝分岐エージェントの連続性と離散性
以上のように連続性/離散性の種類や連続化/離散化について見てきたが、次回は既存の建築物
やプロジェクトに見られる連続性と離散性について考えようと思う。



























